Maatriksi järjestus on oluline numbriline tunnus. Kõige tüüpilisem probleem, mis nõuab maatriksi järgu leidmist, on lineaarsete algebraliste võrrandite süsteemi järjepidevuse kontrollimine. Selles artiklis anname maatriksi astme mõiste ja kaalume selle leidmise meetodeid. Materjali paremaks mõistmiseks analüüsime üksikasjalikult mitme näite lahendusi.

Leheküljel navigeerimine.

Maatriksi järgu määramine ja vajalikud lisamõisted.

Enne maatriksi auastme määratluse väljaütlemist peaksite hästi mõistma alaealise mõistet ja maatriksi alaealiste leidmine eeldab determinandi arvutamise oskust. Seega soovitame vajadusel meelde tuletada artikli teooriat, maatriksi determinandi leidmise meetodeid ja determinandi omadusi.

Võtame maatriksi A järjestusega . Olgu k mingi naturaalarv, mis ei ületa väikseimat arvudest m ja n, see tähendab, .

Definitsioon.

Väike k-s tellimus maatriks A on järjestuse ruutmaatriksi determinant, mis koosneb maatriksi A elementidest, mis paiknevad eelnevalt valitud k reas ja k veerus ning maatriksi A elementide paigutus säilib.

Teisisõnu, kui maatriksist A kustutame (p–k) rida ja (n–k) veerud ning ülejäänud elementidest loome maatriksi, säilitades maatriksi A elementide paigutuse, siis determinant saadud maatriks on maatriksi A järgu k minor.

Vaatame näite abil maatriks-molli definitsiooni.

Mõelge maatriksile .

Paneme kirja selle maatriksi mitu esimest järku molli. Näiteks kui valime maatriksi A kolmanda rea ​​ja teise veeru, vastab meie valik esimest järku minoorile . Teisisõnu, selle minoori saamiseks kriipsutasime maatriksist A maha esimese ja teise rea, samuti esimese, kolmanda ja neljanda veeru ning moodustasime ülejäänud elemendist determinandi. Kui valime maatriksi A esimese rea ja kolmanda veeru, saame minoori .

Illustreerime käsitletavate esimese järgu alaealiste saamise protseduuri
Ja .

Seega on maatriksi esimest järku minoorsed maatriksielemendid ise.

Näitame mitut teist järku alaealist. Valige kaks rida ja kaks veergu. Näiteks võtke esimene ja teine ​​rida ning kolmas ja neljas veerg. Selle valikuga on meil teist järku moll . Selle molli saab koostada ka maatriksist A kolmanda rea, esimese ja teise veeru kustutamisega.

Teine maatriksi A teist järku moll on .

Illustreerime nende teist järku alaealiste ehitust
Ja .

Samamoodi võib leida maatriksi A kolmandat järku minoori. Kuna maatriksis A on ainult kolm rida, valime need kõik. Kui valime nendest ridadest kolm esimest veergu, saame kolmandat järku minoorse

Selle saab konstrueerida ka maatriksi A viimase veeru maha kriipsutades.

Teine kolmanda järgu alaealine on

saadakse maatriksi A kolmanda veeru kustutamisel.

Siin on pilt, mis näitab nende kolmanda järgu alaealiste ehitamist
Ja .

Antud maatriksi A jaoks pole kolmandikust kõrgemat järku minoorseid, kuna .

Mitu k-ndat järgu alaealist on järgu maatriksis A?

K järku alaealiste arvu saab arvutada kui , kus Ja - kombinatsioonide arv vastavalt p-st k-ni ja n-st k-ni.

Kuidas saame maatriksi A kõik järgu p minorid konstrueerida n võrra?

Vajame palju maatriksirea numbreid ja palju veerunumbreid. Kirjutame kõik üles p-elementide kombinatsioonid k-ga(need vastavad maatriksi A valitud ridadele järgu k molli koostamisel). Igale reanumbrite kombinatsioonile lisame järjestikku k veerunumbri n elemendi kombinatsioonid. Need maatriksi A ridade ja veerunumbrite kombinatsioonide komplektid aitavad koostada kõiki k järku minoorseid.

Vaatame seda näitega.

Näide.

Leia kõik maatriksi teist järku mollid.

Lahendus.

Kuna algse maatriksi järjestus on 3 korda 3, on teise järgu alaealiste kogusumma .

Kirjutame üles kõik maatriksi A 3 kuni 2 reanumbrite kombinatsioonid: 1, 2; 1, 3 ja 2, 3. Kõik 3–2 veerunumbrite kombinatsioonid on 1, 2; 1, 3 ja 2, 3.

Võtame maatriksi A esimese ja teise rea. Valides nende ridade jaoks esimese ja teise veeru, esimese ja kolmanda veeru, teise ja kolmanda veeru, saame vastavalt alaealised.

Esimese ja kolmanda rea ​​jaoks on meil sarnase veergude valikuga

Teisele ja kolmandale reale tuleb lisada esimene ja teine, esimene ja kolmas, teine ​​ja kolmas veerg:

Seega on leitud maatriksi A kõik üheksa teist järku minoori.

Nüüd saame jätkata maatriksi auastme määramist.

Definitsioon.

Maatriksi auaste on maatriksi nullist erineva minoori kõrgeim järk.

Maatriksi A astet tähistatakse kui Rank(A) . Võite leida ka tähistusi Rg(A) või Rang(A) .

Maatriksi auaste ja maatriksi väiksemate definitsioonide põhjal võime järeldada, et nullmaatriksi auaste on võrdne nulliga ja nullmaatriksi auaste ei ole väiksem kui üks.

Maatriksi auastme leidmine definitsiooni järgi.

Niisiis, esimene meetod maatriksi auastme leidmiseks on alaealiste loendamise meetod. See meetod põhineb maatriksi järjestuse määramisel.

Peame leidma järjestusmaatriksi A auaste.

Kirjeldame lühidalt algoritm selle probleemi lahendamine alaealiste loetlemisega.

Kui maatriksis on vähemalt üks element, mis erineb nullist, siis on maatriksi auaste vähemalt võrdne ühega (kuna on olemas esimest järku minor, mis ei võrdu nulliga).

Järgmisena vaatame teise järgu alaealisi. Kui kõik teist järku alaealised on võrdsed nulliga, on maatriksi auaste võrdne ühega. Kui teist järku on vähemalt üks nullist erinev moll, siis loetleme kolmanda järgu mollid ja maatriksi auaste on vähemalt võrdne kahega.

Samamoodi, kui kõik kolmanda järgu alaealised on nullid, on maatriksi auaste kaks. Kui on vähemalt üks kolmanda järgu alaealine peale nulli, siis on maatriksi auaste vähemalt kolm ja liigume edasi neljanda järgu alaealiste loendamise juurde.

Pange tähele, et maatriksi auaste ei tohi ületada väikseimat arvu p ja n.

Näide.

Leidke maatriksi auaste .

Lahendus.

Kuna maatriks on nullist erinev, ei ole selle aste väiksem kui üks.

Teise järgu alaealine erineb nullist, seetõttu on maatriksi A aste vähemalt kaks. Liigume edasi kolmanda järgu alaealiste loendamise juurde. Neid kokku asju.

Kõik kolmanda järgu alaealised on võrdsed nulliga. Seetõttu on maatriksi auaste kaks.

Vastus:

Aste(A) = 2 .

Maatriksi auastme leidmine alaealiste ääristamise meetodil.

Maatriksi järgu leidmiseks on ka teisi meetodeid, mis võimaldavad saada tulemuse väiksema arvutustööga.

Üks selline meetod on serva minoor meetod.

Tegeleme ääremolli mõiste.

Öeldakse, et maatriksi A (k+1) järgu moll M ok piirneb maatriksi A järgu k minoorse M-ga, kui minoorsele M ok-le vastav maatriks "sisaldab" mollile vastavat maatriksit. M .

Ehk siis piirnevale mollile M vastav maatriks saadakse piirdemollis M ok vastavast maatriksist, kustutades ühe rea ja ühe veeru elemendid.

Mõelge näiteks maatriksile ja võta teise järgu alaealine. Paneme kirja kõik piirnevad alaealised:

Alaealiste ääristamise meetodit põhjendab järgmine teoreem (esitame selle sõnastuse ilma tõestuseta).

Teoreem.

Kui kõik maatriksi A k-ndat järku minooriga n-ga piirnevad alaealised on võrdsed nulliga, siis kõik maatriksi A järgu (k+1) mollid on võrdsed nulliga.

Seega ei ole maatriksi auastme leidmiseks vaja läbida kõiki alaealisi, mis on piisavalt piirnevad. Järkjärgu maatriksi A k-ndat järku mollidega piirnevate alaealiste arv leitakse valemiga . Pange tähele, et maatriksi A k-ndat järku molli piirnevaid alaealisi ei ole rohkem kui maatriksi A (k + 1) järgu molli. Seetõttu on alaealiste piiritlemise meetodi kasutamine enamasti tulusam kui lihtsalt kõigi alaealiste loetlemine.

Liigume edasi maatriksi auastme leidmisele alaealiste ääristamise meetodil. Kirjeldame lühidalt algoritm seda meetodit.

Kui maatriks A on nullist erinev, siis esimest järku minoorseks võtame maatriksi A mis tahes elemendi, mis erineb nullist. Vaatame selle piirnevaid alaealisi. Kui need kõik on võrdsed nulliga, on maatriksi auaste võrdne ühega. Kui on vähemalt üks nullist erinev piirnev alaealine (selle järjekord on kaks), siis käsitleme selle piirnevaid alaealisi. Kui need kõik on nullid, siis Aste (A) = 2. Kui vähemalt üks piirnev alaealine on nullist erinev (selle järjekord on kolm), siis käsitleme selle piirnevaid alaealisi. Ja nii edasi. Selle tulemusena on Aste(A) = k, kui kõik maatriksi A (k + 1) järku piirnevad alaealised on võrdsed nulliga või Aste(A) = min(p, n), kui on olemas mitte- järgu molliga piirnev null-moll (min( p, n) – 1) .

Vaatame näite abil maatriksi auastme leidmiseks alaealiste ääristamise meetodit.

Näide.

Leidke maatriksi auaste alaealiste piiritlemise meetodil.

Lahendus.

Kuna maatriksi A element a 1 1 on nullist erinev, võtame seda esimest järku minoorsena. Alustame nullist erineva piirneva molli otsimist:

Leitakse teist järku servamoll, mis erineb nullist. Vaatame selle piirnevaid alaealisi (nende asjad):

Kõik teist järku molliga piirnevad alaealised on võrdsed nulliga, seetõttu on maatriksi A aste võrdne kahega.

Vastus:

Aste(A) = 2 .

Näide.

Leidke maatriksi auaste kasutades piirnevaid alaealisi.

Lahendus.

Esimest järku nullist erineva minoorina võtame maatriksi A elemendi a 1 1 = 1. Teise järgu ümberkaudne moll ei ole võrdne nulliga. See alaealine piirneb kolmanda järgu alaealisega
. Kuna see ei ole võrdne nulliga ja selle jaoks pole ühtegi piirnevat molli, võrdub maatriksi A auaste kolmega.

Vastus:

Aste(A) = 3 .

Auastme leidmine elementaarmaatriksteisenduste abil (Gaussi meetod).

Vaatleme teist võimalust maatriksi auastme leidmiseks.

Järgmisi maatriksteisendusi nimetatakse elementaarseteks:

• maatriksi ridade (või veergude) ümberkorraldamine;
• maatriksi mis tahes rea (veeru) kõigi elementide korrutamine suvalise arvuga k, mis erineb nullist;
• rea (veeru) elementidele lisades maatriksi teise rea (veeru) vastavad elemendid, korrutatuna suvalise arvuga k.

Maatriksit B nimetatakse samaväärseks maatriksiga A, kui B saadakse A-st, kasutades lõplikku arvu elementaarteisendusi. Maatriksite samaväärsust tähistatakse sümboliga “~”, st kirjutatud A ~ B.

Maatriksi järgu leidmine elementaarmaatriksteisenduste abil põhineb väitel: kui maatriksist A saadakse maatriksist A lõpliku arvu elementaarteisenduste abil, siis Rank(A) = Aste(B) .

Selle väite kehtivus tuleneb maatriksi determinandi omadustest:

• Maatriksi ridade (või veergude) ümberkorraldamisel muudab selle determinant märki. Kui see on võrdne nulliga, siis ridade (veerude) ümberpaigutamisel jääb see võrdseks nulliga.
• Maatriksi mis tahes rea (veeru) kõigi elementide korrutamisel suvalise arvuga k, mis ei ole null, on saadud maatriksi determinant võrdne algmaatriksi determinandiga, mis on korrutatud k-ga. Kui algse maatriksi determinant on võrdne nulliga, siis pärast mis tahes rea või veeru kõigi elementide korrutamist arvuga k on saadud maatriksi determinant samuti võrdne nulliga.
• Maatriksi teatud rea (veeru) elementide liitmine maatriksi teise rea (veeru) vastavate elementide korrutatuna teatud arvuga k ei muuda selle determinanti.

Elementaarteisenduste meetodi olemus seisneb maatriksi, mille auaste peame leidma, taandamises elementaarteisenduste abil trapetsikujuliseks (konkreetsel juhul ülemiseks kolmnurkseks).

Miks seda tehakse? Seda tüüpi maatriksite järjestust on väga lihtne leida. See võrdub ridade arvuga, mis sisaldavad vähemalt ühte nullist erinevat elementi. Ja kuna maatriksi auaste elementaarsete teisenduste tegemisel ei muutu, on saadud väärtus algse maatriksi auaste.

Toome illustratsioonid maatriksitest, millest üks tuleks saada pärast teisendusi. Nende välimus sõltub maatriksi järjestusest.

Need illustratsioonid on mallid, milleks teisendame maatriksi A.

Kirjeldame meetodi algoritm.

Peame leidma nullist erineva maatriksi A järjestuse (p võib olla võrdne n-ga).

Niisiis, . Korrutame maatriksi A esimese rea kõik elemendid . Sel juhul saame samaväärse maatriksi, mis tähistab seda A (1):

Saadud maatriksi A (1) teise rea elementidele liidame esimese rea vastavad elemendid, korrutatuna . Kolmanda rea ​​elementidele liidame esimese rea vastavad elemendid, korrutatuna . Ja nii edasi kuni p-nda reani. Võtame samaväärse maatriksi, tähistame seda A (2):

Kui kõik saadud maatriksi elemendid, mis asuvad ridades teisest kuni p-ndani, on võrdsed nulliga, on selle maatriksi auaste võrdne ühega ja sellest tulenevalt on algse maatriksi aste võrdne ühele.

Kui ridades teisest kuni p-ndani on vähemalt üks nullist erinev element, jätkame teisenduste läbiviimist. Pealegi toimime täpselt samamoodi, kuid ainult joonisel märgitud maatriksi A (2) osaga.

Kui , siis korraldame maatriksi A (2) read ja (või) veerud ümber nii, et “uus” element muutub nullist erinevaks.

Maatriksi astme kontseptsiooniga töötamiseks vajame teavet teemast "Algebralised täiendid ja minoorsed lisandid. Minoride tüübid ja algebralised täiendid." Esiteks puudutab see terminit "matrix minor", kuna me määrame maatriksi auastme täpselt alaealiste kaudu.

Maatriksi auaste on selle alaealiste maksimaalne järjestus, mille hulgas on vähemalt üks, mis ei ole võrdne nulliga.

Samaväärsed maatriksid- maatriksid, mille auastmed on üksteisega võrdsed.

Selgitame üksikasjalikumalt. Oletame, et teist järku alaealiste hulgas on vähemalt üks, mis erineb nullist. Ja kõik alaealised, kelle järjekord on suurem kui kaks, on võrdsed nulliga. Järeldus: maatriksi auaste on 2 või näiteks kümnenda järgu alaealiste seas on vähemalt üks, mis ei ole võrdne nulliga. Ja kõik alaealised, kelle järjekord on suurem kui 10, on võrdsed nulliga. Järeldus: maatriksi auaste on 10.

Maatriksi $A$ järjestust tähistatakse järgmiselt: $\rang A$ või $r(A)$. Nullmaatriksi $O$ auaste eeldatakse nulliks, $\rang O=0$. Tuletan meelde, et maatriksi molli moodustamiseks tuleb read ja veerud läbi kriipsutada, kuid pole võimalik maha kriipsutada rohkem ridu ja veerge, kui maatriks ise sisaldab. Näiteks kui maatriksi $F$ suurus on $5\ korda 4$ (st sisaldab 5 rida ja 4 veergu), siis on selle alatähtede maksimaalne järjekord neli. Viienda järgu alaealisi ei ole enam võimalik moodustada, kuna nende jaoks on vaja 5 veergu (ja meil on ainult 4). See tähendab, et maatriksi $F$ auaste ei saa olla suurem kui neli, s.t. $\rang F≤4$.

Üldisemas vormis tähendab eeltoodu, et kui maatriks sisaldab $m$ rida ja $n$ veergu, siis ei saa selle aste ületada $m$ ja $n$ väikseimat, s.t. $\rang A≤\min(m,n)$.

Põhimõtteliselt tuleneb auastme määratlusest selle leidmise meetod. Maatriksi järgu leidmise protsessi saab definitsiooni järgi skemaatiliselt kujutada järgmiselt:

Lubage mul seda diagrammi üksikasjalikumalt selgitada. Alustame arutlemist päris algusest, st. mõne maatriksi $A$ esimese järgu alaealistest.

1. Kui kõik esimest järku minoorsed (st maatriksi $A$ elemendid) on võrdsed nulliga, siis $\rang A=0$. Kui esimest järku alaealiste hulgas on vähemalt üks, mis ei ole võrdne nulliga, siis $\rang A≥ 1$. Liigume edasi teise järgu alaealiste kontrollimise juurde.
2. Kui kõik teist järku alaealised on võrdsed nulliga, siis $\rang A=1$. Kui teist järku alaealiste hulgas on vähemalt üks, mis ei ole võrdne nulliga, siis $\rang A≥ 2$. Liigume edasi kolmanda järgu alaealiste kontrollimise juurde.
3. Kui kõik kolmandat järku alaealised on võrdsed nulliga, siis $\rang A=2$. Kui kolmandat järku alaealiste hulgas on vähemalt üks, mis ei ole võrdne nulliga, siis $\rang A≥ 3$. Liigume edasi neljanda järgu alaealiste kontrollimise juurde.
4. Kui kõik neljandat järku alaealised on võrdsed nulliga, siis $\rang A=3$. Kui neljandat järku alaealiste hulgas on vähemalt üks, mis ei ole võrdne nulliga, siis $\rang A≥ 4$. Liigume edasi viienda järgu alaealiste kontrollimisele ja nii edasi.

Mis ootab meid selle protseduuri lõpus? Võimalik, et k-ndat järku alaealiste hulgas on vähemalt üks, mis erineb nullist, ja kõik (k+1) järgu alaealised on võrdsed nulliga. See tähendab, et k on alaealiste maksimaalne järjekord, mille hulgas on vähemalt üks, mis ei võrdu nulliga, s.t. auaste võrdub k-ga. Olukord võib olla erinev: k-ndat järku alaealiste hulgas on vähemalt üks, mis ei võrdu nulliga, kuid (k+1) järgu alaealisi enam moodustada ei saa. Sel juhul võrdub maatriksi auaste ka k-ga. Lühidalt, viimati koostatud nullist erineva molli järjekord võrdub maatriksi auastmega.

Liigume edasi näidete juurde, milles illustreeritakse selgelt maatriksi astme leidmise protsessi definitsiooni järgi. Rõhutan veel kord, et selle teema näidetes hakkame maatriksite auastet leidma ainult auastme definitsiooni abil. Teistest meetoditest (maatriksi auastme arvutamine alaealiste piiritlemise meetodil, maatriksi auastme arvutamine elementaarteisenduste meetodil) käsitletakse järgmistes teemades.

Muide, auastme leidmise protseduuri pole üldse vaja alustada kõige väiksemat järku alaealistega, nagu tehti näidetes nr 1 ja nr 2. Saate kohe liikuda kõrgema järgu alaealiste juurde (vt näide nr 3).

Näide nr 1

Leidke maatriksi auaste $A=\left(\begin(massiivi)(ccccc) 5 & 0 & -3 & 0 & 2 \\ 7 & 0 & -4 & 0 & 3 \\ 2 & 0 & -1 & 0 & 1 \end(massiivi) \right)$.

Selle maatriksi suurus on $3\ korda 5 $, st. sisaldab kolme rida ja viit veergu. Arvudest 3 ja 5 on miinimum 3, seetõttu ei ole maatriksi $A$ auaste suurem kui 3, s.o. $\rang A≤ 3$. Ja see ebavõrdsus on ilmne, kuna me ei saa enam moodustada neljandat järku alaealisi - nende jaoks on vaja 4 rida ja meil on ainult 3. Liigume otse antud maatriksi auastme leidmise protsessi juurde.

Esimest järku alaealiste hulgas (s.o. maatriksi $A$ elementide hulgas) on nullist erinevad ühed. Näiteks 5, -3, 2, 7. Üldiselt ei huvita meid nullist erinevate elementide koguarv. Seal on vähemalt üks nullist erinev element - ja sellest piisab. Kuna esimest järku alaealiste hulgas on vähemalt üks nullist erinev, järeldame, et $\rang A≥ 1$ ja jätkame teist järku alaealiste kontrollimist.

Alustame teise järgu alaealiste uurimist. Näiteks ridade nr 1, nr 2 ja veergude nr 1, nr 4 ristumiskohas on järgmise alaea elemendid: $\left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(massiiv) \right|. Selle determinandi puhul on kõik teise veeru elemendid võrdsed nulliga, seetõttu on determinant ise võrdne nulliga, s.t. $\left|\begin(massiivi)(cc) 5 & 0 \\ 7 & 0 \end(massiivi) \right|=0$ (vt omadus nr 3 determinantide omaduste teemas). Või võite lihtsalt arvutada selle determinandi, kasutades valemit nr 1, mis on esitatud teist ja kolmandat järku determinantide arvutamise jaotises:

$$ \left|\begin(massiivi)(cc) 5 & 0 \\ 7 & 0 \end(massiivi) \right|=5\cdot 0-0\cdot 7=0. $$

Esimene teist järku moll, mida testisime, osutus nulliga võrdseks. Mida see tähendab? Teise järgu alaealiste täiendava kontrollimise vajadusest. Kas need kõik osutuvad nulliks (ja siis võrdub auaste 1-ga) või on nende hulgas vähemalt üks alaealine, mis erineb nullist. Proovime teha parema valiku, kirjutades teist järku molli, mille elemendid asuvad ridade nr 1, nr 2 ning veergude nr 1 ja nr 5 ristumiskohas: $\left|\begin( massiiv)(cc) 5 & 2 \\ 7 & 3 \end(massiivi) \right|$. Leiame selle teist järku molli väärtuse:

$$ \left|\begin(massiivi)(cc) 5 & 2 \\ 7 & 3 \end(massiivi) \right|=5\cdot 3-2\cdot 7=1. $$

See alaealine ei ole võrdne nulliga. Järeldus: teist järku alaealiste hulgas on vähemalt üks nullist erinev. Seetõttu $\rang A≥ 2$. Peame üle minema kolmanda järgu alaealiste õppimisele.

Kui valime kolmandat järku alaealiste moodustamiseks veeru nr 2 või veeru nr 4, siis on sellised alaealised võrdsed nulliga (kuna need sisaldavad nulli veergu). Jääb üle kontrollida ainult üks kolmanda järgu alaealine, mille elemendid asuvad veergude nr 1, nr 3, nr 5 ja ridade nr 1, nr 2, nr 3 ristumiskohas. Kirjutame selle molli üles ja leiame selle väärtuse:

$$ \left|\begin(massiivi)(ccc) 5 & -3 & 2 \\ 7 & -4 & 3 \\ 2 & -1 & 1 \end(massiivi) \right|=-20-18-14 +16+21+15=0. $$

Seega on kõik kolmanda järgu alaealised võrdsed nulliga. Viimane nullist erinev moll, mille me koostasime, oli teist järku. Järeldus: alaealiste maksimaalne järjekord, mille hulgas on vähemalt üks nullist erinev, on 2. Seega $\rang A=2$.

Vastus: $\rang A=2$.

Näide nr 2

Leidke maatriksi auaste $A=\left(\begin(massiivi) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0 \\ 9 & 7 & 8 & -7 \end(massiivi) \right)$.

Meil on neljandat järku ruutmaatriks. Pangem kohe tähele, et selle maatriksi aste ei ületa 4, s.o. $\rang A≤ 4$. Alustame maatriksi auastme leidmist.

Esimest järku minoorsete (st maatriksi $A$ elementide hulgas) on vähemalt üks, mis ei ole võrdne nulliga, seega $\rang A≥ 1$. Liigume edasi teise järgu alaealiste kontrollimise juurde. Näiteks ridade nr 2, nr 3 ning veergude nr 1 ja nr 2 ristumiskohas saame järgmise teist järku minoori: $\left| \begin(massiivi) (cc) 4 & -2 \\ -5 & 0 \end(massiivi) \right|$. Arvutame selle välja:

$$\left| \begin(massiivi) (cc) 4 & -2 \\ -5 & 0 \end(massiivi) \right|=0-10=-10. $$

Teist järku alaealiste hulgas on vähemalt üks, mis ei ole võrdne nulliga, seega $\rang A≥ 2$.

Liigume edasi kolmanda järgu alaealiste juurde. Leiame näiteks alaealise, mille elemendid asuvad ridade nr 1, nr 3, nr 4 ja veergude nr 1, nr 2, nr 4 ristumiskohas:

$$\left | \begin(massiivi) (cccc) -1 & 3 & -3\\ -5 & 0 & 0\\ 9 & 7 & -7 \end(massiivi) \right|=105-105=0. $$

Kuna see kolmanda järgu alaealine osutus võrdseks nulliga, on vaja uurida veel üht kolmandat järku alaealist. Kas kõik need on võrdsed nulliga (siis võrdub auaste 2) või nende hulgas on vähemalt üks, mis ei ole võrdne nulliga (siis hakkame õppima neljanda järgu alaealisi). Vaatleme kolmandat järku minoorset, mille elemendid asuvad ridade nr 2, nr 3, nr 4 ja veergude nr 2, nr 3, nr 4 ristumiskohas:

$$\left| \begin(massiivi) (ccc) -2 & 5 & 1\\ 0 & -4 & 0\\ 7 & 8 & -7 \end(massiivi) \right|=-28. $$

Kolmandat järku alaealiste hulgas on vähemalt üks nullist erinev, seega $\rang A≥ 3$. Liigume edasi neljanda järgu alaealiste kontrollimise juurde.

Iga neljandat järku minoor asub maatriksi $A$ nelja rea ​​ja nelja veeru ristumiskohas. Teisisõnu, neljandat järku moll on maatriksi $A$ determinant, kuna see maatriks sisaldab 4 rida ja 4 veergu. Selle maatriksi determinant arvutati välja näites nr 2 teemast "Determinandi järjekorra vähendamine reas (veerus)", seega võtame lihtsalt valmis tulemuse:

$$\left| \begin(massiivi) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end (massiivi)\right|=86. $$

Seega ei võrdu neljanda järgu moll nulliga. Viiendat järku alaealisi me enam moodustada ei saa. Järeldus: alaealiste kõrgeim järjekord, mille hulgas on vähemalt üks nullist erinev, on 4. Tulemus: $\rang A=4$.

Vastus: $\rang A=4$.

Näide nr 3

Leidke maatriksi auaste $A=\left(\begin(massiivi) (cccc) -1 & 0 & 2 & -3\\ 4 & -2 & 5 & 1\\ 7 & -4 & 0 & -5 \end( massiiv) \right)$.

Pangem kohe tähele, et see maatriks sisaldab 3 rida ja 4 veergu, seega $\rang A≤ 3$. Eelmistes näidetes alustasime auastme leidmist kõige väiksema (esimese) järgu alaealiste arvessevõtmisega. Siin püüame kohe kontrollida alaealisi kõrgeima võimaliku järjekorraga. Maatriksi $A$ jaoks on need kolmanda järgu alaealised. Vaatleme kolmandat järku molli, mille elemendid asuvad ridade nr 1, nr 2, nr 3 ja veergude nr 2, nr 3, nr 4 ristumiskohas:

$$\left| \begin(massiivi) (ccc) 0 & 2 & -3\\ -2 & 5 & 1\\ -4 & 0 & -5 \end(massiivi) \right|=-8-60-20=-88. $$

Seega on alaealiste kõrgeim järjekord, mille hulgas on vähemalt üks, mis ei ole võrdne nulliga, 3. Seetõttu on maatriksi auaste 3, s.o. $\rang A=3$.

Vastus: $\rang A=3$.

Üldiselt on maatriksi astme leidmine definitsiooni järgi üldiselt üsna töömahukas ülesanne. Näiteks suhteliselt väikeses maatriksis, mille suurus on $5\x4$, on 60 teist järku alaealist. Ja isegi kui 59 neist võrdub nulliga, võib 60. moll osutuda nullist erinevaks. Siis peate õppima kolmanda järgu kõrvalerialasid, millest selles maatriksis on 40 tükki. Tavaliselt püütakse kasutada vähem tülikaid meetodeid, nagu alaealiste piiritlemise meetod või samaväärsete teisenduste meetod.

Vaatleme ka teema olulist praktilist rakendust: lineaarvõrrandi süsteemi uurimine järjepidevuse tagamiseks.

Mis on maatriksi auaste?

Artikli humoorikas epigraaf sisaldab suures koguses tõtt. Tavaliselt seostame sõna "aste" mingisuguse hierarhiaga, kõige sagedamini karjääriredeliga. Mida rohkem on inimesel teadmisi, kogemusi, võimeid, sidemeid jne. – mida kõrgem on tema positsioon ja võimalused. Noorte mõistes viitab auaste üldisele "järsusele".

Ja meie matemaatilised vennad elavad samade põhimõtete järgi. Teeme mõned suvalised jalutama nullmaatriksid:

Mõelgem sellele, kui maatriksis kõik nullid, siis millisest auastmest saame rääkida? Kõik on tuttavad mitteametliku väljendiga “kogu null”. Maatriksite ühiskonnas on kõik täpselt sama:

Nullmaatriksi astemis tahes suurus võrdub nulliga.

Märge : Nullmaatriksit tähistatakse kreeka tähega "teeta"

Maatriksi auastme paremaks mõistmiseks kasutan edaspidi abiks materjale analüütiline geomeetria. Arvesta nulliga vektor meie kolmemõõtmeline ruum, mis ei määra kindlat suunda ja on ehitamiseks kasutu afiinne alus. Algebralisest vaatenurgast on selle vektori koordinaadid sisse kirjutatud maatriks"üks-kolm" ja loogiline (näidatud geomeetrilises tähenduses) eeldame, et selle maatriksi aste on null.

Vaatame nüüd mõnda nullist erinev veeruvektorid Ja rea vektorid:


Igal eksemplaril on vähemalt üks nullist erinev element ja see on midagi!

Iga nullist erineva reavektori (veeruvektor) auaste on võrdne ühega

Ja üldiselt - kui maatriksis suvalised suurused on vähemalt üks nullist erinev element, siis selle järk mitte vähemühikut.

Algebralised reavektorid ja veeruvektorid on teatud määral abstraktsed, seega pöördume uuesti geomeetrilise seose poole. Mitte-null vektor määrab ruumis väga kindla suuna ja sobib konstrueerimiseks alus, seetõttu loetakse maatriksi auaste võrdseks ühega.

Teoreetiline teave : lineaaralgebras on vektor vektorruumi element (määratletud 8 aksioomi kaudu), mis võib eelkõige kujutada reaalarvude järjestatud rida (või veergu) reaalarvuga liitmise ja korrutamise operatsioonidega. neile. Täpsemat teavet vektorite kohta leiate artiklist Lineaarsed teisendused.

lineaarselt sõltuv(väljendatakse üksteise kaudu). Geomeetrilisest vaatenurgast sisaldab teine ​​rida kollineaarse vektori koordinaate , mis ehituses asja üldse edasi ei viinud kolmemõõtmeline alus, olles selles mõttes üleliigne. Seega on selle maatriksi auaste ka võrdne ühega.

Kirjutame vektorite koordinaadid ümber veergudeks ( maatriksi transponeerimiseks):

Mis on auastme osas muutunud? Mitte midagi. Veerud on proportsionaalsed, mis tähendab, et auaste on võrdne ühega. Muide, pange tähele, et kõik kolm rida on ka proportsionaalsed. Neid saab koordinaatide abil tuvastada kolm tasapinna kollineaarsed vektorid, millest ainult üks kasulik "lameda" aluse ehitamiseks. Ja see on täielikult kooskõlas meie geomeetrilise auastmetajuga.

Ülaltoodud näitest tuleneb oluline väide:

Maatriksi järjestus ridades on võrdne maatriksi järjestusega veergudes. Mainisin seda juba veidi tõhusate õppetükis determinandi arvutamise meetodid.

Märge : ridade lineaarne sõltuvus eeldab veergude lineaarset sõltuvust (ja vastupidi). Kuid aja säästmiseks ja harjumusest räägin ma peaaegu alati stringide lineaarsest sõltuvusest.

Jätkame oma armastatud lemmiklooma treenimist. Lisame kolmanda rea ​​maatriksile veel ühe kollineaarse vektori koordinaadid :

Kas ta aitas meid kolmemõõtmelise aluse ehitamisel? Muidugi mitte. Kõik kolm vektorit kõnnivad mööda sama rada edasi-tagasi ja maatriksi auaste on võrdne ühega. Võite võtta nii palju kollineaarseid vektoreid kui soovite, näiteks 100, panna nende koordinaadid maatriksisse "sada korda kolm" ja sellise pilvelõhkuja auaste jääb ikkagi üheks.

Tutvume maatriksiga, mille read lineaarselt sõltumatu. Kolmemõõtmelise aluse konstrueerimiseks sobib paar mittekollineaarset vektorit. Selle maatriksi auaste on kaks.

Mis on maatriksi auaste? Jooned ei tundu olevat proportsionaalsed... nii et teoreetiliselt on neid kolm. Selle maatriksi auaste on aga samuti kaks. Lisasin kaks esimest rida ja kirjutasin tulemuse alla, st. lineaarselt väljendatud kolmas rida läbi kahe esimese. Geomeetriliselt vastavad maatriksi read kolme koordinaatidele koplanaarsed vektorid, ja nende kolme hulgas on paar mittekollineaarset seltsimeest.

Nagu sa näed, lineaarne sõltuvus vaadeldavas maatriksis pole ilmne ja täna õpime, kuidas see avalikkuse ette tuua.

Ma arvan, et paljud inimesed võivad arvata, mis on maatriksi auaste!

Vaatleme maatriksit, mille read lineaarselt sõltumatu. Vektorid moodustuvad afiinne alus ja selle maatriksi auaste on kolm.

Nagu teate, väljendatakse kolmemõõtmelise ruumi mis tahes neljandat, viiendat, kümnendat vektorit lineaarselt baasvektorites. Seega, kui lisate maatriksile suvalise arvu ridu, siis selle auaste võrdub ikkagi kolmega.

Sarnaseid arutlusi saab läbi viia ka suuremate maatriksite puhul (loomulikult ilma geomeetrilise tähenduseta).

Definitsioon : Maatriksi järjestus on lineaarselt sõltumatute ridade maksimaalne arv. Või: Maatriksi järjestus on lineaarselt sõltumatute veergude maksimaalne arv. Jah, nende arv on alati sama.

Eeltoodust tuleneb ka oluline praktiline juhend: maatriksi aste ei ületa selle minimaalset mõõdet. Näiteks maatriksis neli rida ja viis veergu. Minimaalne mõõde on neli, seetõttu ei ületa selle maatriksi aste kindlasti 4.

Nimetused: maailma teoorias ja praktikas pole maatriksi auastme määramiseks üldtunnustatud standardit; enamasti võite leida: - nagu öeldakse, inglane kirjutab üht, sakslane teist. Seetõttu, tuginedes kuulsale naljale Ameerika ja Venemaa põrgu kohta, tähistame maatriksi auastet emakeelse sõnaga. Näiteks: . Ja kui maatriks on "nimetu", mida on palju, võite lihtsalt kirjutada .

Kuidas leida alaealiste abil maatriksi auastet?

Kui mu vanaemal oleks maatriksis viies veerg, siis ta peaks arvutama teise 4. järgu alaealise (“sinine”, “vaarikas” + 5. veerg).

Järeldus: nullist erineva molli maksimaalne järjekord on kolm, mis tähendab .

Võib-olla pole kõik sellest fraasist täielikult aru saanud: 4. järku alaealine on võrdne nulliga, kuid 3. järgu alaealiste hulgas oli nullist erinev üks - seega maksimumjärk nullist erinev minoorne ja võrdub kolmega.

Tekib küsimus, miks mitte kohe determinant välja arvutada? Noh, esiteks, enamikus ülesannetes pole maatriks ruudukujuline ja teiseks, isegi kui saate nullist erineva väärtuse, lükatakse ülesanne tõenäoliselt tagasi, kuna see hõlmab tavaliselt tavalist alt-üles lahendust. Ja vaadeldavas näites võimaldab 4. järgu nulldeterminant väita, et maatriksi auaste on ainult väiksem kui neli.

Pean tunnistama, et mõtlesin probleemile, mida ise analüüsisin, et paremini selgitada alaealiste piirnemise meetodit. Tegelikus praktikas on kõik lihtsam:

Näide 2

Leidke maatriksi auaste servamollide meetodi abil

Lahendus ja vastus on tunni lõpus.

Millal töötab algoritm kõige kiiremini? Tuleme tagasi sama neli korda nelja maatriksi juurde. . Ilmselgelt on "hea" puhul lahendus lühim nurga alaealised:

Ja kui , siis , muidu – .

Mõtlemine pole sugugi hüpoteetiline – on palju näiteid, kus kogu asi piirdub ainult nurgeliste alaealistega.

Kuid mõnel juhul on mõni muu meetod tõhusam ja eelistatavam:

Kuidas leida maatriksi auastet Gaussi meetodi abil?

Lõik on mõeldud lugejatele, kes on sellega juba tuttavad Gaussi meetod ja sai enam-vähem kätte.

Tehnilisest vaatenurgast ei ole meetod uudne:

1) elementaarteisenduste abil taandame maatriksi astmelisele kujule;

2) maatriksi järjestus võrdub ridade arvuga.

See on täiesti selge Gaussi meetodi kasutamine ei muuda maatriksi auastet, ja olemus on siin äärmiselt lihtne: vastavalt algoritmile tuvastatakse ja eemaldatakse elementaarsete teisenduste käigus kõik mittevajalikud proportsionaalsed (lineaarselt sõltuvad) read, mille tulemuseks on "kuiv jääk" - maksimaalne lineaarselt sõltumatute ridade arv.

Teisendame vana tuttava maatriksi kolme kollineaarse vektori koordinaatidega:

(1) Esimene rida liideti teisele reale, korrutatuna -2-ga. Esimene rida lisati kolmandale reale.

(2) Nulljooned eemaldatakse.

Seega on jäänud üks rida, seega . Ütlematagi selge, et see on palju kiirem, kui arvutada 2. järku üheksa null-molli ja alles seejärel teha järeldus.

Tuletan teile seda iseenesest meelde algebraline maatriks midagi muuta ei saa ja teisendusi tehakse ainult auastme määramise eesmärgil! Muide, peatume veel kord küsimusel, miks mitte? Allikamaatriks 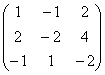kannab infot, mis põhimõtteliselt erineb maatriksi ja rea ​​informatsioonist. Mõnes matemaatilises mudelis (ei ole liialdus) võib ühe arvu erinevus olla elu ja surma küsimus. ...meenusid alg- ja keskkooli matemaatikaõpetajad, kes pisimagi ebatäpsuse või algoritmist kõrvalekaldumise eest halastamatult hindeid 1-2 punkti võrra kärpisid. Ja see oli kohutav pettumus, kui näiliselt garanteeritud “A” asemel tuli välja “hea” või veelgi hullem. Arusaam tuli palju hiljem – kuidas muidu satelliite, tuumalõhkepäid ja elektrijaamu inimese kätte usaldada? Aga ärge muretsege, ma ei tööta nendel aladel =)

Liigume edasi sisukamate ülesannete juurde, kus muuhulgas tutvume oluliste arvutustehnikatega Gaussi meetod:

Näide 3

Leidke maatriksi auaste elementaarteisenduste abil

Lahendus: antakse maatriks "neli korda viis", mis tähendab, et selle aste ei ole kindlasti suurem kui 4.

Esimeses veerus ei ole 1 ega –1, seetõttu on vähemalt ühe ühiku saamiseks vaja täiendavaid toiminguid. Kogu saidi olemasolu jooksul on mulle korduvalt küsitud küsimust: "Kas elementaarsete teisenduste ajal on võimalik veerge ümber paigutada?" Siin korraldasime esimese ja teise veeru ümber ning kõik on korras! Enamikus ülesannetes, kus seda kasutatakse Gaussi meetod, saab veerge tõepoolest ümber paigutada. KUID POLE VAJA. Ja asi pole isegi mitte muutujatega võimalikus segaduses, asi on selles, et kõrgema matemaatika klassikalises kursuses seda toimingut traditsiooniliselt ei arvestata, seega vaadatakse sellist noogutust VÄGA viltu (või isegi sunnitakse kõike uuesti tegema).

Teine punkt puudutab numbreid. Otsuse tegemisel on kasulik järgida järgmist rusikareeglit: elementaarteisendused peaksid võimalusel vähendama maatriksiarve. Lõppude lõpuks on palju lihtsam töötada ühe, kahe, kolmega kui näiteks numbritega 23, 45 ja 97. Ja esimene toiming ei ole suunatud mitte ainult esimeses veerus oleva ühe saamisele, vaid ka numbrite kõrvaldamisele. 7 ja 11.

Kõigepealt terviklahendus, seejärel kommentaarid:

(1) Esimene rida liideti teisele reale, korrutatuna -2-ga. Esimene rida lisati kolmandale reale, korrutatuna -3-ga. Ja kuhja juurde: 1. rida liideti 4. reale, korrutati –1-ga.

(2) Kolm viimast rida on võrdelised. 3. ja 4. rida eemaldati, teine ​​rida viidi esimesele kohale.

(3) Esimene rida liideti teisele reale, korrutatuna -3-ga.

Ešelonikujuliseks taandatud maatriksil on kaks rida.

Vastus:

Nüüd on teie kord neli korda neli maatriksit piinata:

Näide 4

Leidke maatriksi auaste Gaussi meetodi abil

Ma tuletan teile seda meelde Gaussi meetod ei tähenda ühemõttelist jäikust ja teie otsus erineb tõenäoliselt minu otsusest. Lühike näide ülesandest tunni lõpus.

Millist meetodit peaksin kasutama maatriksi auastme leidmiseks?

Praktikas pole sageli üldse öeldud, millist meetodit auastme leidmiseks kasutada. Sellises olukorras tuleks analüüsida tingimust - mõne maatriksi puhul on ratsionaalsem lahendada alaealiste kaudu, samas kui teiste jaoks on palju tulusam rakendada elementaarseid teisendusi:

Näide 5

Leidke maatriksi auaste

Lahendus: esimene meetod kaob kuidagi kohe ära =)

Natuke kõrgemal soovitasin maatriksi veerge mitte puudutada, aga kui on null veerg ehk proportsionaalsed/kattuvad veerud, siis tasub ikka amputeerida:

(1) Viies veerg on null, eemaldage see maatriksist. Seega pole maatriksi auaste suurem kui neli. Esimene rida korrutati -1-ga. See on veel üks Gaussi meetodi tunnusomadus, mis muudab järgmise toimingu meeldivaks jalutuskäiguks:

(2) Kõigile ridadele, alates teisest, lisati esimene rida.

(3) Esimene rida korrutati –1-ga, kolmas rida jagati 2-ga, neljas rida 3-ga. Viiendale reale liideti teine ​​rida, korrutati –1-ga.

(4) Viiendale reale liideti kolmas rida, korrutatuna -2-ga.

(5) Kaks viimast rida on proportsionaalsed, viies jäetakse välja.

Tulemuseks on 4 rida.

Vastus:

Standardne viiekorruseline hoone iseseisvaks õppeks:

Näide 6

Leidke maatriksi auaste

Lühilahendus ja vastus tunni lõpus.

Tuleb märkida, et väljendit "maatriksi auaste" praktikas nii sageli ei näe ja enamiku probleemide puhul saate ilma selleta täiesti hakkama. Kuid on üks ülesanne, kus kõnealune kontseptsioon on peategelane, ja me lõpetame artikli selle praktilise rakendusega:

Kuidas uurida lineaarvõrrandisüsteemi järjepidevuse tagamiseks?

Sageli lisaks lahendusele lineaarvõrrandisüsteemid tingimuse kohaselt tuleb esmalt kontrollida selle ühilduvust, st tõestada, et lahendus on üldse olemas. Sellises kontrollis mängib võtmerolli Kroneckeri-Capelli teoreem, mille sõnastan vajalikul kujul:

Kui auaste süsteemsed maatriksid võrdne auastmega laiendatud maatrikssüsteem, siis on süsteem järjekindel ja kui see arv langeb kokku tundmatute arvuga, siis on lahendus kordumatu.

Seega on süsteemi ühilduvuse uurimiseks vaja kontrollida võrdsust , Kus - süsteemi maatriks(pidage meeles tunni terminoloogiat Gaussi meetod), A - laiendatud süsteemimaatriks(ehk maatriks muutujate koefitsientidega + vabade terminite veerg).

Elementaarne Nimetatakse järgmisi maatriksteisendusi:

1) mis tahes kahe rea (või veeru) permutatsioon,

2) rea (või veeru) korrutamine nullist erineva arvuga,

3) ühele reale (või veerule) teise rea (või veeru) lisamine, korrutades teatud arvuga.

Neid kahte maatriksit nimetatakse samaväärne, kui üks neist saadakse teisest elementaarteisenduste lõpliku hulga abil.

Ekvivalentmaatriksid ei ole üldiselt võrdsed, kuid nende auastmed on võrdsed. Kui maatriksid A ja B on samaväärsed, siis kirjutatakse see järgmiselt: A ~ B.

Kanooniline Maatriks on maatriks, milles põhidiagonaali alguses on reas mitu ühte (mille arv võib olla null) ja kõik muud elemendid on võrdsed nulliga, näiteks

Kasutades ridade ja veergude elementaarseid teisendusi, saab mis tahes maatriksi taandada kanooniliseks. Kanoonilise maatriksi aste on võrdne selle põhidiagonaalil olevate maatriksite arvuga.

Näide 2 Leidke maatriksi auaste

A=

ja viige see kanoonilisse vormi.

Lahendus. Teisest reast lahutage esimene ja korraldage need read ümber:

.

Nüüd lahutame teisest ja kolmandast reast esimese, korrutatuna vastavalt 2 ja 5-ga:

;

lahutage esimene kolmandast reast; saame maatriksi

B = ,

mis on ekvivalentne maatriksiga A, kuna see saadakse sellest elementaarteisenduste lõpliku hulga abil. Ilmselgelt on maatriksi B aste 2 ja seega r(A)=2. Maatriksi B saab hõlpsasti taandada kanooniliseks. Lahutades kõigist järgnevatest esimese veeru, mis on korrutatud sobivate arvudega, nullisime kõik esimese rea elemendid, välja arvatud esimene, ja ülejäänud ridade elemendid ei muutu. Seejärel, lahutades kõigist järgnevatest teise veeru, mis on korrutatud sobivate arvudega, nullisime kõik teise rea elemendid, välja arvatud teine, ja saame kanoonilise maatriksi:

.

Kronecker – Capelli teoreem- lineaarsete algebraliste võrrandite süsteemi ühilduvuse kriteerium:

Selleks, et lineaarne süsteem oleks järjepidev, on vajalik ja piisav, et selle süsteemi laiendatud maatriksi auaste oleks võrdne selle põhimaatriksi astmega.

Tõend (süsteemi ühilduvustingimused)

Vajadus

Lase süsteem liigend Siis on sellised numbrid, et . Seetõttu on veerg maatriksi veergude lineaarne kombinatsioon. Sellest, et maatriksi auaste ei muutu, kui selle ridade (veergude) süsteemist kustutatakse või lisatakse rida (veerg), mis on teiste ridade (veergude) lineaarne kombinatsioon, järeldub, et .

Adekvaatsus

Laske . Võtame maatriksis mõned põhimollid. Sellest ajast alates on see ka maatriksi alusmoll. Siis vastavalt alusteoreemile alaealine, on maatriksi viimane veerg baasveergude, st maatriksi veergude lineaarne kombinatsioon. Seetõttu on süsteemi vabaliikmete veerg maatriksi veergude lineaarne kombinatsioon.

Tagajärjed

Peamiste muutujate arv süsteemid võrdne süsteemi auastmega.

Ühine süsteem defineeritakse (selle lahendus on kordumatu), kui süsteemi auaste on võrdne kõigi selle muutujate arvuga.

Homogeenne võrrandisüsteem

Pakkumine15 . 2 Homogeenne võrrandisüsteem

on alati ühine.

Tõestus. Selle süsteemi jaoks on lahenduseks arvude hulk , , .

Selles osas kasutame süsteemi maatrikstähistust: .

Pakkumine15 . 3 Homogeense lineaarvõrrandisüsteemi lahendite summa on selle süsteemi lahendus. Lahendus, mis on korrutatud arvuga, on samuti lahendus.

Tõestus. Las need toimivad süsteemi lahendustena. Siis ja. Laske . Siis

Sellest ajast peale – lahendus.

Laskma olema suvaline arv, . Siis

Sellest ajast peale – lahendus.

Tagajärg15 . 1 Kui homogeensel lineaarvõrrandisüsteemil on nullist erinev lahend, siis on sellel lõpmatult palju erinevaid lahendeid.

Tõepoolest, korrutades nullist erineva lahenduse erinevate arvudega, saame erinevad lahendid.

Definitsioon15 . 5 Me ütleme, et lahendused süsteemid moodustavad põhiline lahenduste süsteem, kui veerud moodustavad lineaarselt sõltumatu süsteemi ja süsteemi mis tahes lahendus on nende veergude lineaarne kombinatsioon.

Selles artiklis käsitletakse sellist mõistet nagu maatriksi auaste ja vajalikud lisamõisted. Toome näiteid ja tõendeid maatriksi auastme leidmise kohta ning räägime ka sellest, mis on maatriks-moll ja miks see nii oluline on.

Yandex.RTB R-A-339285-1

Maatriks-moll

Et mõista, mis on maatriksi auaste, peate mõistma maatriksi molli mõistet.

Definitsioon 1

Alaealinekmaatriksi järjekord on k×k suurusjärgu ruutmaatriksi determinant, mis koosneb maatriksi A elementidest, mis paiknevad eelnevalt valitud k-ridades ja k-veerudes, säilitades maatriksi A elementide asukoha.

Lihtsamalt öeldes, kui maatriksis A kustutate (p-k) read ja (n-k) veerud ning allesjäänud elementidest loote maatriksi, säilitades maatriksi A elementide paigutuse, siis on saadud maatriksi determinant maatriksi A järk k-moll.

Näitest järeldub, et maatriksi A esimest järku minoorid on maatriksielemendid ise.

Võime tuua mitu näidet 2. järku alaealistest. Valime kaks rida ja kaks veergu. Näiteks 1. ja 2. rida, 3. ja 4. veerg.

Selle elementide valiku korral on teist järku minor - 1 3 0 2 = (- 1) × 2 - 3 × 0 = - 2

Teine maatriksi A teist järku minoor on 0 0 1 1 = 0

Toome illustratsioonid maatriksi A teist järku minoorsete konstruktsioonide kohta:

Kolmandat järku minoori saamiseks kriipsutatakse maha maatriksi A kolmas veerg:

0 0 3 1 1 2 - 1 - 4 0 = 0 × 1 × 0 + 0 × 2 × (- 1) + 3 × 1 × (- 4) - 3 × 1 × (- 1) - 0 × 1 × 0 – 0 × 2 × (– 4) = – 9

Illustratsioon maatriksi A 3. järku minoori saamisest:

Antud maatriksi puhul pole 3. järku kõrgemaid alaealisi, sest

k ≤ m i n (p , n) = m i n (3, 4) = 3

Mitu k-järku minoorset on maatriksil A järku p×n?

Alaealiste arv arvutatakse järgmise valemi abil:

C p k × C n k , kus e C p k = p ! k! (p - k) ! ja C n k = n ! k! (n - k) ! - kombinatsioonide arv vastavalt p-st k-ni, n-st k-ni.

Pärast seda, kui oleme kindlaks teinud, millised on maatriksi A minoorid, saame jätkata maatriksi A järgu määramisega.

Maatriksiaste: leidmise meetodid

2. definitsioon

Maatriksi auaste - maatriksi kõrgeim järjekord peale nulli.

Nimetus 1

Aste (A), Rg (A), vahemik (A).

Maatriksi auaste ja maatriksi minoori määratlusest selgub, et nullmaatriksi auaste on võrdne nulliga ja nullmaatriksi auaste erineb nullist.

Maatriksi auastme leidmine definitsiooni järgi

3. definitsioon

Alaealiste loendamise meetod - maatriksi järgu määramisel põhinev meetod.

Toimingute algoritm alaealiste loendamise meetodil :

On vaja leida järjestusmaatriksi A aste lk× n. Kui on vähemalt üks nullist erinev element, on maatriksi auaste vähemalt võrdne ühega ( sest on 1. järku molli, mis ei võrdu nulliga).

Edasi tuleb II järgu alaealiste loendamine. Kui kõik 2. järgu alaealised on võrdsed nulliga, siis on auaste võrdne ühega. Kui on vähemalt üks nullist erinev 2. järku moll, tuleb liikuda edasi 3. järgu alaealiste loendamise juurde ja maatriksi auaste on sel juhul võrdne vähemalt kahega.

Teeme sama ka 3. järgu auastmega: kui maatriksi kõik alaealised on nulliga, siis võrdub auaste kahega. Kui on vähemalt üks nullist erinev 3. järku moll, siis on maatriksi auaste vähemalt kolm. Ja nii edasi, analoogia põhjal.

Näide 2

Leidke maatriksi auaste:

A = - 1 1 - 1 - 2 0 2 2 6 0 - 4 4 3 11 1 - 7

Kuna maatriks on nullist erinev, on selle minimaalne aste üks.

2. järku moll - 1 1 2 2 = (- 1) × 2 - 1 × 2 = 4 on nullist erinev. Sellest järeldub, et maatriksi A aste on vähemalt kaks.

Sorteerime välja 3. järgu alaealised: C 3 3 × C 5 3 = 1 5! 3! (5-3)! = 10 tükki.

1 1 - 1 2 2 6 4 3 11 = (- 1) × 2 × 11 + 1 × 6 × 4 + (- 1) × 2 × 3 - (- 1) × 2 × 4 - 1 × 2 × 11 - (- 1) × 6 × 3 = 0

1 - 1 - 2 2 6 0 4 11 1 = (- 1) × 6 × 1 + (- 1) × 0 × 4 + (- 2) × 2 × 11 - (- 2) × 6 × 4 - (- 1) × 2 × 1 – (- 1) × 0 × 11 = 0

1 1 - 2 2 2 0 4 3 1 = (- 1) × 2 × 1 + 1 × 0 × 4 + (- 2) × 2 × 3 - (- 2) × 2 × 4 - 1 × 2 × 1 - (- 1) × 0 × 3 = 0

1 - 1 0 2 6 - 4 4 11 - 7 = (- 1) × 6 × (- 7) + (- 1) × (- 4) × 4 + 0 × 2 × 11 - 0 × 6 × 4 - ( - 1) × 2 × (- 7) - (- 1) × (- 4) × 11 = 0

1 - 1 0 2 6 - 4 3 11 - 7 = 1 × 6 × (- 7) + (- 1) × (- 4) × 3 + 0 × 2 × 11 - 0 × 6 × 3 - (- 1) × 2 × (- 7) - 1 × (- 4) × 11 = 0

1 - 2 0 2 0 - 4 3 1 - 7 = 1 × 0 × (- 7) + (- 2) × (- 4) × 3 + 0 × 2 × 1 - 0 × 0 × 3 - (- 2) × 2 × (- 7) - 1 × (- 4) × 1 = 0

1 - 2 0 6 0 - 4 11 1 - 7 = (- 1) × 0 × (- 7) + (- 2) × (- 4) × 11 + 0 × 6 × 1 - 0 × 0 × 11 - ( - 2) × 6 × (- 7) - (- 1) × (- 4) × 1 = 0

Kolmanda järgu alaealised on võrdsed nulliga, seega on maatriksi auaste kaks.

Vastus : Aste (A) = 2.

Maatriksi auastme leidmine ääristavate alaealiste meetodil

3. definitsioon

Piiritav minoormeetod - meetod, mis võimaldab saada tulemusi väiksema arvutustööga.

Serv minoor - maatriksi A järgu moll M o k (k + 1), mis piirneb maatriksi A järgu k minoorse M-ga, kui mollile M o k vastav maatriks “sisaldab” maatriksile vastavat maatriksit. alaealine M.

Lihtsamalt öeldes saadakse ääristavale mollile M vastav maatriks ääristavale mollile M o k vastavast maatriksist, kustutades ühe rea ja ühe veeru elemendid.

Näide 3

Leidke maatriksi auaste:

A = 1 2 0 - 1 3 - 2 0 3 7 1 3 4 - 2 1 1 0 0 3 6 5

Auastme leidmiseks võtame 2. järku molli M = 2 - 1 4 1

Kirjutame üles kõik piirnevad alaealised:

1 2 - 1 - 2 0 7 3 4 1 , 2 0 - 1 0 3 7 4 - 2 1 , 2 - 1 3 0 7 1 4 1 1 , 1 2 - 1 3 4 1 0 0 6 , 2 0 - 1 4 - 2 1 0 3 6 , 2 - 1 3 4 1 1 0 6 5 .

Põhjendamaks alaealiste piiritlemise meetodit, esitame teoreemi, mille sõnastamine ei vaja tõestust.

1. teoreem

Kui kõik maatriksi A k-ndat järku minooriga n-ga piirnevad alaealised on võrdsed nulliga, siis kõik maatriksi A järgu (k+1) mollid on võrdsed nulliga.

Toimingute algoritm :

Maatriksi auastme leidmiseks pole vaja kõiki alaealisi läbida, piisab, kui vaadata piirnevaid.

Kui piirnevad alaealised on võrdsed nulliga, on maatriksi auaste null. Kui on vähemalt üks alaealine, mis ei ole võrdne nulliga, siis käsitleme piirnevaid alaealisi.

Kui need kõik on nullid, on Aste(A) kaks. Kui on vähemalt üks nullist erinev alaealine, siis käsitleme selle piirnevaid alaealisi. Ja nii edasi, samamoodi.

Näide 4

Leidke maatriksi auaste servamollide meetodi abil

A = 2 1 0 - 1 3 4 2 1 0 - 1 2 1 1 1 - 4 0 0 2 4 - 14

Kuidas lahendada?

Kuna maatriksi A element a 11 ei ole võrdne nulliga, võtame 1. järku molli. Hakkame otsima ääristavat alaealist, mis erineb nullist:

2 1 4 2 = 2 × 2 - 1 × 4 = 0 2 0 4 1 = 2 × 1 - 0 × 4 = 2

Leidsime 2. järku piirneva molli, mis ei ole võrdne nulliga 2 0 4 1 .

Loetleme piirnevad alaealised - (neid on (4 - 2) × (5 - 2) = 6 tükki).

2 1 0 4 2 1 2 1 1 = 0 ; 2 0 - 1 4 1 0 2 1 1 = 0 ; 2 0 3 4 1 - 1 2 1 - 4 = 0 ; 2 1 0 4 2 1 0 0 2 = 0 ; 2 0 - 1 4 1 0 0 2 4 = 0 ; 2 0 3 4 1 - 1 0 2 - 14 = 0

Vastus : Aste(A) = 2.

Maatriksi järgu leidmine Gaussi meetodi abil (kasutades elementaarteisendusi)

Meenutagem, mis on elementaarsed teisendused.

Elementaarsed teisendused:

• maatriksi ridade (veergude) ümberpaigutamise teel;
• korrutades maatriksi mis tahes rea (veeru) kõik elemendid suvalise nullist erineva arvuga k;

lisades mis tahes rea (veeru) elementidele maatriksi teisele reale (veerule) vastavad elemendid, mis korrutatakse suvalise arvuga k.

Definitsioon 5

Maatriksi järgu leidmine Gaussi meetodil - meetod, mis põhineb maatriksi ekvivalentsuse teoorial: kui maatriksist A saadakse maatriks B, kasutades lõplikku arvu elementaarteisendusi, siis Rank(A) = Rank(B).

Selle väite kehtivus tuleneb maatriksi definitsioonist:

• Kui maatriksi read või veerud on ümber paigutatud, muudab selle determinant märki. Kui see on võrdne nulliga, siis ridade või veergude ümberkorraldamisel jääb see võrdseks nulliga;
• kui maatriksi mis tahes rea (veeru) kõik elemendid korrutatakse suvalise arvuga k, mis ei ole võrdne nulliga, on saadud maatriksi determinant võrdne algmaatriksi determinandiga, mis korrutatakse k;

maatriksi teatud rea või veeru elementidele liitmisel teise rea või veeru vastavad elemendid, mis on korrutatud arvuga k, ei muuda selle determinanti.

Elementaarteisenduste meetodi olemus : taandada maatriks, mille järk on vaja leida, trapetsikujuliseks, kasutades elementaarteisendusi.

Milleks?

Seda tüüpi maatriksite järjestust on üsna lihtne leida. See võrdub ridade arvuga, millel on vähemalt üks nullist erinev element. Ja kuna auaste elementaarsete teisenduste tegemisel ei muutu, on see maatriksi auaste.

Illustreerime seda protsessi:

• ristkülikukujuliste maatriksite A puhul, mille ridade arv on suurem kui veergude arv:

A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 2 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 010n 1 0 0 0 ⋯ 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0, R a n k (A) = n

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ k + 0 k + 1 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0, R a n k (A) = k

• ristkülikukujuliste maatriksite A puhul, mille ridade arv on väiksem kui veergude arv:

A ~ 1 b 12 b 13 ⋯ b 1 p b 1 p + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 p b 2 p + 1 ⋯ b 2 n b ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ + 0 p 0 1 ⋯ b p n , R a n k (A) = p

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ k + 0 k + 1 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0

• ruutmaatriksite A jaoks, mille suurusjärk on n korda n:

A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 1 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 010n 1 , R a n k (A) = n

A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ k + 0 k + 1 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0, R a n k (A) = k, k< n

Näide 5

Leidke maatriksi A aste elementaarteisenduste abil:

A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11

Kuidas lahendada?

Kuna element a 11 erineb nullist, on vaja maatriksi A esimese rea elemendid korrutada 1 a 11 = 1 2-ga:

A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~

Lisame 2. rea elementidele 1. rea vastavad elemendid, mis korrutatakse (-3). 3. rea elementidele lisame 1. rea elemendid, mis korrutatakse (-1):

~ A (1) = 1 1 2 - 1 3 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~ A (2) = = 1 1 2 - 1 3 3 + 1 (- 3) 0 + 1 2 (- 3) 0 + (- 1) (- 3) - 1 + 3 (- 3) 1 + 1 (- 3) - 1 + 1 2 (- 3) 2 + (- 1) (- 1) - 7 + 3 (- 1) 5 + 1 (- 5) - 2 + 1 2 (- 5) 4 + (- 1) (- 5) - 15 + 3 (- 5) 7 + 1 (- 7) 2 + 1 2 (- 7) - 4 + (- 1) (- 7) 11 + 3 (- 7) =

1 1 2 - 1 3 0 - 3 2 3 - 10 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10

Element a 22 (2) on nullist erinev, seega korrutame maatriksi A 2. rea elemendid A (2)-ga 1 a 22 (2) = - 2 3:

A (3) = 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10 ~ A (4) = 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 0 - 9 2 + 1 9 2 9 + (- 2) 9 2 - 30 + 20 3 × 9 2 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 = = 1 1 2 - 1 3 0 1 - 2 20 3 0 0 0 0 0 0 0 0 0 0 0 0

• Saadud maatriksi 3. rea elementidele lisame 2. rea vastavad elemendid, mis korrutatakse 3 2-ga;
• 4. rea elementide juurde - 2. rea elemendid, mis korrutatakse 9 2-ga;
• 5. rea elementide juurde - 2. rea elemendid, mis korrutatakse 3 2-ga.

Kõik rea elemendid on nullid. Seega viisime elementaarteisenduste abil maatriksi trapetsikujulisele kujule, millest on näha, et R an k (A (4)) = 2. Sellest järeldub, et algse maatriksi auaste on samuti võrdne kahega.

Kommenteeri

Kui teete elementaarseid teisendusi, pole ligikaudsed väärtused lubatud!

Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter