Lesson and presentation on the topic: "Systems of equations. Substitution method, addition method, method of introducing a new variable"
Additional materials
Dear users, do not forget to leave your comments, reviews, wishes! All materials have been checked by an anti-virus program.
Educational aids and simulators in the Integral online store for grade 9
Simulator for textbooks by Atanasyan L.S. Simulator for textbooks Pogorelova A.V.
Methods for solving systems of inequalities
Guys, we have studied systems of equations and learned how to solve them using graphs. Now let's see what other ways to solve systems exist?Almost all the methods for solving them are no different from those we studied in 7th grade. Now we need to make some adjustments according to the equations that we have learned to solve.
The essence of all methods described in this lesson, this is the replacement of a system with an equivalent system with more simple view and the method of solution. Guys, remember what an equivalent system is.
Substitution method
The first way to solve systems of equations with two variables is well known to us - this is the substitution method. We used this method to solve linear equations. Now let's see how to solve equations in the general case?How should you proceed when making a decision?
1. Express one of the variables in terms of another. The variables most often used in equations are x and y. In one of the equations we express one variable in terms of another. Tip: Look at both equations carefully before you start solving, and choose the one where it is easier to express the variable.
2. Substitute the resulting expression into the second equation, instead of the variable that was expressed.
3. Solve the equation that we got.
4. Substitute the resulting solution into the second equation. If there are several solutions, then you need to substitute them sequentially so as not to lose a couple of solutions.
5. As a result, you will receive a pair of numbers $(x;y)$, which must be written down as an answer.
Example.
Solve a system with two variables using the substitution method: $\begin(cases)x+y=5, \\xy=6\end(cases)$.
Solution.
Let's take a close look at our equations. Obviously, expressing y in terms of x in the first equation is much simpler.
$\begin(cases)y=5-x, \\xy=6\end(cases)$.
Let's substitute the first expression into the second equation $\begin(cases)y=5-x, \\x(5-2x)=6\end(cases)$.
Let's solve the second equation separately:
$x(5-x)=6$.
$-x^2+5x-6=0$.
$x^2-5x+6=0$.
$(x-2)(x-3)=0$.
We obtained two solutions to the second equation $x_1=2$ and $x_2=3$.
Substitute successively into the second equation.
If $x=2$, then $y=3$. If $x=3$, then $y=2$.
The answer will be two pairs of numbers.
Answer: $(2;3)$ and $(3;2)$.
Algebraic addition method
We also studied this method in 7th grade.It is known that rational equation from two variables we can multiply by any number, not forgetting to multiply both sides of the equation. We multiplied one of the equations by a certain number so that when adding the resulting equation to the second equation of the system, one of the variables was destroyed. Then the equation was solved for the remaining variable.
This method still works, although it is not always possible to destroy one of the variables. But it allows you to significantly simplify the form of one of the equations.
Example.
Solve the system: $\begin(cases)2x+xy-1=0, \\4y+2xy+6=0\end(cases)$.
Solution.
Let's multiply the first equation by 2.
$\begin(cases)4x+2xy-2=0, \\4y+2xy+6=0\end(cases)$.
Let's subtract the second from the first equation.
$4x+2xy-2-4y-2xy-6=4x-4y-8$.
As you can see, the form of the resulting equation is much simpler than the original one. Now we can use the substitution method.
$\begin(cases)4x-4y-8=0, \\4y+2xy+6=0\end(cases)$.
Let's express x in terms of y in the resulting equation.
$\begin(cases)4x=4y+8, \\4y+2xy+6=0\end(cases)$.
$\begin(cases)x=y+2, \\4y+2(y+2)y+6=0\end(cases)$.
$\begin(cases)x=y+2, \\4y+2y^2+4y+6=0\end(cases)$.
$\begin(cases)x=y+2, \\2y^2+8y+6=0\end(cases)$.
$\begin(cases)x=y+2, \\y^2+4y+3=0\end(cases)$.
$\begin(cases)x=y+2, \\(y+3)(y+1)=0\end(cases)$.
We got $y=-1$ and $y=-3$.
Let's substitute these values sequentially into the first equation. We get two pairs of numbers: $(1;-1)$ and $(-1;-3)$.
Answer: $(1;-1)$ and $(-1;-3)$.
Method for introducing a new variable
We also studied this method, but let's look at it again.Example.
Solve the system: $\begin(cases)\frac(x)(y)+\frac(2y)(x)=3, \\2x^2-y^2=1\end(cases)$.
Solution.
Let us introduce the replacement $t=\frac(x)(y)$.
Let's rewrite the first equation with a new variable: $t+\frac(2)(t)=3$.
Let's solve the resulting equation:
$\frac(t^2-3t+2)(t)=0$.
$\frac((t-2)(t-1))(t)=0$.
We got $t=2$ or $t=1$. Let us introduce the reverse change $t=\frac(x)(y)$.
We got: $x=2y$ and $x=y$.
For each of the expressions, the original system must be solved separately:
$\begin(cases)x=2y, \\2x^2-y^2=1\end(cases)$. $\begin(cases)x=y, \\2x^2-y^2=1\end(cases)$.
$\begin(cases)x=2y, \\8y^2-y^2=1\end(cases)$. $\begin(cases)x=y, \\2y^2-y^2=1\end(cases)$.
$\begin(cases)x=2y, \\7y^2=1\end(cases)$. $\begin(cases)x=2y, \\y^2=1\end(cases)$.
$\begin(cases)x=2y, \\y=±\frac(1)(\sqrt(7))\end(cases)$. $\begin(cases)x=y, \\y=±1\end(cases)$.
$\begin(cases)x=±\frac(2)(\sqrt(7)), \\y=±\frac(1)(\sqrt(7))\end(cases)$. $\begin(cases)x=±1, \\y=±1\end(cases)$.
We received four pairs of solutions.
Answer: $(\frac(2)(\sqrt(7));\frac(1)(\sqrt(7)))$; $(-\frac(2)(\sqrt(7));-\frac(1)(\sqrt(7)))$; $(1;1)$; $(-1;-1)$.
Example.
Solve the system: $\begin(cases)\frac(2)(x-3y)+\frac(3)(2x+y)=2,\\\frac(8)(x-3y)-\frac(9 )(2x+y)=1\end(cases)$.
Solution.
Let us introduce the replacement: $z=\frac(2)(x-3y)$ and $t=\frac(3)(2x+y)$.
Let's rewrite the original equations with new variables:
$\begin(cases)z+t=2, \\4z-3t=1\end(cases)$.
Let's use the algebraic addition method:
$\begin(cases)3z+3t=6, \\4z-3t=1\end(cases)$.
$\begin(cases)3z+3t+4z-3t=6+1, \\4z-3t=1\end(cases)$.
$\begin(cases)7z=7, \\4z-3t=1\end(cases)$.
$\begin(cases)z=1, \\-3t=1-4\end(cases)$.
$\begin(cases)z=1, \\t=1\end(cases)$.
Let's introduce the reverse substitution:
$\begin(cases)\frac(2)(x-3y)=1, \\\frac(3)(2x+y)=1\end(cases)$.
$\begin(cases)x-3y=2, \\2x+y=3\end(cases)$.
Let's use the substitution method:
$\begin(cases)x=2+3y, \\4+6y+y=3\end(cases)$.
$\begin(cases)x=2+3y, \\7y=-1\end(cases)$.
$\begin(cases)x=2+3(\frac(-1)(7)), \\y=\frac(-1)(7)\end(cases)$.
$\begin(cases)x=\frac(11)(7), \\x=-\frac(11)(7)\end(cases)$.
Answer: $(\frac(11)(7);-\frac(1)(7))$.
Problems on systems of equations for independent solution
Solve systems:1. $\begin(cases)2x-2y=6,\\xy =-2\end(cases)$.
2. $\begin(cases)x+y^2=3, \\xy^2=4\end(cases)$.
3. $\begin(cases)xy+y^2=3,\\y^2-xy=5\end(cases)$.
4. $\begin(cases)\frac(2)(x)+\frac(1)(y)=4, \\\frac(1)(x)+\frac(3)(y)=9\ end(cases)$.
5. $\begin(cases)\frac(5)(x^2-xy)+\frac(4)(y^2-xy)=-\frac(1)(6), \\\frac(7 )(x^2-xy)-\frac(3)(y^2-xy)=\frac(6)(5)\end(cases)$. Lesson content
Linear equations in two variables
A schoolchild has 200 rubles to eat lunch at school. A cake costs 25 rubles, and a cup of coffee costs 10 rubles. How many cakes and cups of coffee can you buy for 200 rubles?
Let us denote the number of cakes by x, and the number of cups of coffee through y. Then the cost of the cakes will be denoted by the expression 25 x, and the cost of cups of coffee in 10 y .
25x— price x cakes
10y — price y cups of coffee
The total amount should be 200 rubles. Then we get an equation with two variables x And y
25x+ 10y= 200
How many roots does this equation have?
It all depends on the student’s appetite. If he buys 6 cakes and 5 cups of coffee, then the roots of the equation will be the numbers 6 and 5.
The pair of values 6 and 5 are said to be the roots of equation 25 x+ 10y= 200 . Written as (6; 5), with the first number being the value of the variable x, and the second - the value of the variable y .
6 and 5 are not the only roots that reverse equation 25 x+ 10y= 200 to identity. If desired, for the same 200 rubles a student can buy 4 cakes and 10 cups of coffee:
In this case, the roots of equation 25 x+ 10y= 200 is a pair of values (4; 10).
Moreover, a schoolchild may not buy coffee at all, but buy cakes for the entire 200 rubles. Then the roots of equation 25 x+ 10y= 200 will be the values 8 and 0
Or vice versa, don’t buy cakes, but buy coffee for the entire 200 rubles. Then the roots of equation 25 x+ 10y= 200 the values will be 0 and 20
Let's try to list everything possible roots equations 25 x+ 10y= 200 . Let us agree that the values x And y belong to the set of integers. And let these values be greater than or equal to zero:
x∈Z, y∈ Z;
x ≥ 0, y ≥ 0
This will be convenient for the student himself. It is more convenient to buy whole cakes than, for example, several whole cakes and half a cake. It is also more convenient to take coffee in whole cups than, for example, several whole cups and half a cup.
Note that for odd x it is impossible to achieve equality under any circumstances y. Then the values x the following numbers will be 0, 2, 4, 6, 8. And knowing x can be easily determined y
Thus, we received the following pairs of values (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). These pairs are solutions or roots of Equation 25 x+ 10y= 200. They turn this equation into an identity.
Equation of the form ax + by = c called linear equation with two variables. The solution or roots of this equation are a pair of values ( x; y), which turns it into identity.
Note also that if a linear equation with two variables is written in the form ax + b y = c , then they say that it is written in canonical(normal) form.
Some linear equations in two variables can be reduced to canonical form.
For example, the equation 2(16x+ 3y − 4) = 2(12 + 8x − y) can be brought to mind ax + by = c. Let's open the brackets on both sides of this equation and get 32x + 6y − 8 = 24 + 16x − 2y . We group terms containing unknowns on the left side of the equation, and terms free of unknowns - on the right. Then we get 32x− 16x+ 6y+ 2y = 24 + 8 . We present similar terms in both sides, we get equation 16 x+ 8y= 32. This equation is reduced to the form ax + by = c and is canonical.
Equation 25 discussed earlier x+ 10y= 200 is also a linear equation with two variables in canonical form. In this equation the parameters a , b And c are equal to the values 25, 10 and 200, respectively.
Actually the equation ax + by = c has countless solutions. Solving the equation 25x+ 10y= 200, we looked for its roots only on the set of integers. As a result, we obtained several pairs of values that turned this equation into an identity. But on many rational numbers equation 25 x+ 10y= 200 will have infinitely many solutions.
To obtain new pairs of values, you need to take an arbitrary value for x, then express y. For example, let's take for the variable x value 7. Then we get an equation with one variable 25×7 + 10y= 200 in which one can express y
Let x= 15. Then the equation 25x+ 10y= 200 becomes 25 × 15 + 10y= 200. From here we find that y = −17,5
Let x= −3 . Then the equation 25x+ 10y= 200 becomes 25 × (−3) + 10y= 200. From here we find that y = −27,5
System of two linear equations with two variables
For the equation ax + by = c you can take arbitrary values for as many times as you like x and find values for y. Taken separately, such an equation will have countless solutions.
But it also happens that the variables x And y connected not by one, but by two equations. In this case they form the so-called system linear equations with two variables. Such a system of equations can have one pair of values (or in other words: “one solution”).
It may also happen that the system has no solutions at all. A system of linear equations can have countless solutions in rare and exceptional cases.
Two linear equations form a system when the values x And y enter into each of these equations.
Let's go back to the very first equation 25 x+ 10y= 200 . One of the pairs of values for this equation was the pair (6; 5) . This is a case when for 200 rubles you could buy 6 cakes and 5 cups of coffee.
Let's formulate the problem so that the pair (6; 5) becomes the only solution for equation 25 x+ 10y= 200 . To do this, let’s create another equation that would connect the same x cakes and y cups of coffee.
Let us state the text of the problem as follows:
“The student bought several cakes and several cups of coffee for 200 rubles. A cake costs 25 rubles, and a cup of coffee costs 10 rubles. How many cakes and cups of coffee did the student buy, if it is known that the number of cakes per unit more quantity cups of coffee?
We already have the first equation. This is equation 25 x+ 10y= 200 . Now let's create an equation for the condition “the number of cakes is one unit greater than the number of cups of coffee” .
The number of cakes is x, and the number of cups of coffee is y. You can write this phrase using the equation x−y= 1. This equation will mean that the difference between cakes and coffee is 1.
x = y+ 1 . This equation means that the number of cakes is one more than the number of cups of coffee. Therefore, to obtain equality, one is added to the number of cups of coffee. This can be easily understood if we use the model of scales that we considered when studying the simplest problems:
We got two equations: 25 x+ 10y= 200 and x = y+ 1. Since the values x And y, namely 6 and 5 are included in each of these equations, then together they form a system. Let's write down this system. If the equations form a system, then they are framed by the system sign. The system symbol is a curly brace:
Let's decide this system. This will allow us to see how we arrive at the values 6 and 5. There are many methods for solving such systems. Let's look at the most popular of them.
Substitution method
The name of this method speaks for itself. Its essence is to substitute one equation into another, having previously expressed one of the variables.
In our system, nothing needs to be expressed. In the second equation x = y+ 1 variable x already expressed. This variable is equal to the expression y+ 1 . Then you can substitute this expression into the first equation instead of the variable x
After substituting the expression y+ 1 into the first equation instead x, we get the equation 25(y+ 1) + 10y= 200 . This is a linear equation with one variable. This equation is quite easy to solve:
We found the value of the variable y. Now let's substitute this value into one of the equations and find the value x. For this it is convenient to use the second equation x = y+ 1 . Let’s substitute the value into it y
This means that the pair (6; 5) is a solution to the system of equations, as we intended. We check and make sure that the pair (6; 5) satisfies the system:
Example 2
Let's substitute the first equation x= 2 + y into the second equation 3 x− 2y= 9. In the first equation the variable x equal to the expression 2 + y. Let’s substitute this expression into the second equation instead of x
Now let's find the value x. To do this, let's substitute the value y into the first equation x= 2 + y
This means that the solution to the system is the pair value (5; 3)
Example 3. Solve the following system of equations using the substitution method:
Here, unlike previous examples, one of the variables is not expressed explicitly.
To substitute one equation into another, you first need .
It is advisable to express the variable that has a coefficient of one. The variable has a coefficient of one x, which is contained in the first equation x+ 2y= 11. Let's express this variable.
After variable expression x, our system will take the following form:
Now let's substitute the first equation into the second and find the value y
Let's substitute y x
This means that the solution to the system is a pair of values (3; 4)
Of course, you can also express a variable y. This will not change the roots. But if you express y, The result is not a very simple equation, which will take more time to solve. It will look like this:
We see that in in this example express x much more convenient than expressing y .
Example 4. Solve the following system of equations using the substitution method:
Let us express in the first equation x. Then the system will take the form:
y
Let's substitute y into the first equation and find x. You can use the original equation 7 x+ 9y= 8, or use the equation in which the variable is expressed x. We will use this equation because it is convenient:
This means that the solution to the system is a pair of values (5; −3)
Addition method
The addition method consists of adding the equations included in the system term by term. This addition results in a new equation with one variable. And solving such an equation is quite simple.
Let's solve the following system of equations:
Let's add the left side of the first equation with the left side of the second equation. A right side first equation with right side second equation. We get the following equality:
Let's look at similar terms:
As a result, we got the simplest equation 3 x= 27 whose root is 9. Knowing the value x you can find the value y. Let's substitute the value x into the second equation x−y= 3 . We get 9 − y= 3 . From here y= 6 .
This means that the solution to the system is a pair of values (9; 6)
Example 2
Let's add the left side of the first equation with the left side of the second equation. And the right side of the first equation with the right side of the second equation. In the resulting equality we present similar terms:
As a result, we got the simplest equation 5 x= 20, whose root is 4. Knowing the value x you can find the value y. Let's substitute the value x into the first equation 2 x+y= 11. Let's get 8+ y= 11. From here y= 3 .
This means that the solution to the system is a pair of values (4;3)
The addition process is not described in detail. It must be done mentally. When adding, both equations must be reduced to canonical form. That is, by the way ac + by = c .
From the examples considered, it is clear that the main purpose of adding equations is to get rid of one of the variables. But it is not always possible to immediately solve a system of equations using the addition method. Most often, the system is first brought to a form in which the equations included in this system can be added.
For example, the system 
can be solved immediately by addition. When adding both equations, the terms y And −y will disappear because their sum is zero. As a result, the simplest equation 11 is formed x= 22, whose root is 2. It will then be possible to determine y equal to 5.
And the system of equations 
The addition method cannot be solved immediately, since this will not lead to the disappearance of one of the variables. Addition will result in equation 8 x+ y= 28, which has an infinite number of solutions.
If both sides of the equation are multiplied or divided by the same number, not equal to zero, you get an equation equivalent to the given one. This rule is also true for a system of linear equations with two variables. One of the equations (or both equations) can be multiplied by any number. The result will be an equivalent system, the roots of which will coincide with the previous one.
Let's return to the very first system, which described how many cakes and cups of coffee a schoolchild bought. The solution to this system was a pair of values (6; 5).
Let's multiply both equations included in this system by some numbers. Let's say we multiply the first equation by 2, and the second by 3
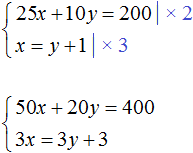
As a result, we got a system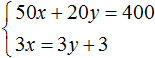 
The solution to this system is still the pair of values (6; 5)
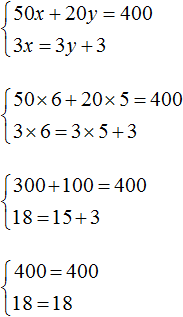
This means that the equations included in the system can be reduced to a form suitable for applying the addition method.
Let's return to the system , which we could not solve using the addition method.
Multiply the first equation by 6, and the second by −2
Then we get the following system:
Let's add up the equations included in this system. Adding components 12 x and −12 x will result in 0, addition 18 y and 4 y will give 22 y, and adding 108 and −20 gives 88. Then we get equation 22 y= 88, from here y = 4 .
If at first it’s hard to add equations in your head, then you can write down how it adds up left side of the first equation with the left side of the second equation, and the right side of the first equation with the right side of the second equation:
Knowing that the value of the variable y equals 4, you can find the value x. Let's substitute y into one of the equations, for example into the first equation 2 x+ 3y= 18. Then we get an equation with one variable 2 x+ 12 = 18. Let's move 12 to the right side, changing the sign, we get 2 x= 6, from here x = 3 .
Example 4. Solve the following system of equations using the addition method:
Let's multiply the second equation by −1. Then the system will take the following form:
Let's add both equations. Adding components x And −x will result in 0, addition 5 y and 3 y will give 8 y, and adding 7 and 1 gives 8. The result is equation 8 y= 8 whose root is 1. Knowing that the value y equals 1, you can find the value x .
Let's substitute y into the first equation, we get x+ 5 = 7, hence x= 2
Example 5. Solve the following system of equations using the addition method:
It is desirable that terms containing the same variables be located one below the other. Therefore, in the second equation the terms 5 y and −2 x Let's swap places. As a result, the system will take the form:
Let's multiply the second equation by 3. Then the system will take the form:
Now let's add both equations. As a result of addition we obtain equation 8 y= 16, whose root is 2.
Let's substitute y into the first equation, we get 6 x− 14 = 40. Let's move the term −14 to the right side, changing the sign, and get 6 x= 54 . From here x= 9.
Example 6. Solve the following system of equations using the addition method:
Let's get rid of fractions. Multiply the first equation by 36, and the second by 12
In the resulting system 
the first equation can be multiplied by −5, and the second by 8
Let's add up the equations in the resulting system. Then we get the simplest equation −13 y= −156 . From here y= 12. Let's substitute y into the first equation and find x
Example 7. Solve the following system of equations using the addition method:
Let us bring both equations to normal form. Here it is convenient to apply the rule of proportion in both equations. If in the first equation the right side is represented as , and the right side of the second equation as , then the system will take the form:
We have a proportion. Let's multiply its extreme and middle terms. Then the system will take the form:
Let's multiply the first equation by −3, and open the brackets in the second:
Now let's add both equations. As a result of adding these equations, we get an equality with zero on both sides:
It turns out that the system has countless solutions.
But we can’t just take arbitrary values from the sky for x And y. We can specify one of the values, and the other will be determined depending on the value we specify. For example, let x= 2 . Let's substitute this value into the system:
As a result of solving one of the equations, the value for y, which will satisfy both equations:
The resulting pair of values (2; −2) will satisfy the system:
Let's find another pair of values. Let x= 4. Let's substitute this value into the system:
You can tell by eye that the value y equals zero. Then we get a pair of values (4; 0) that satisfies our system:
Example 8. Solve the following system of equations using the addition method:
Multiply the first equation by 6, and the second by 12
Let's rewrite what's left:
Let's multiply the first equation by −1. Then the system will take the form:
Now let's add both equations. As a result of addition, equation 6 is formed b= 48, whose root is 8. Substitute b into the first equation and find a
System of linear equations with three variables
A linear equation with three variables includes three variables with coefficients, as well as an intercept term. In canonical form it can be written as follows:
ax + by + cz = d
This equation has countless solutions. Giving two variables different meanings, a third value can be found. The solution in this case is a triple of values ( x; y; z) which turns the equation into an identity.
If the variables x, y, z are interconnected by three equations, then a system of three linear equations with three variables is formed. To solve such a system, you can use the same methods that apply to linear equations with two variables: the substitution method and the addition method.
Example 1. Solve the following system of equations using the substitution method:
Let us express in the third equation x. Then the system will take the form:
Now let's do the substitution. Variable x is equal to the expression 3 − 2y − 2z . Let's substitute this expression into the first and second equations:
Let's open the brackets in both equations and present similar terms:
We have arrived at a system of linear equations with two variables. In this case, it is convenient to use the addition method. As a result, the variable y will disappear and we can find the value of the variable z
Now let's find the value y. To do this, it is convenient to use the equation − y+ z= 4. Substitute the value into it z
Now let's find the value x. To do this, it is convenient to use the equation x= 3 − 2y − 2z . Let's substitute the values into it y And z
Thus, the triple of values (3; −2; 2) is a solution to our system. By checking we make sure that these values satisfy the system:
Example 2. Solve the system using the addition method
Let's add the first equation with the second, multiplied by −2.
If the second equation is multiplied by −2, it takes the form −6x+ 6y − 4z = −4 . Now let's add it to the first equation:
We see that as a result of elementary transformations, the value of the variable was determined x. It is equal to one.
Let's go back to main system. Let's add the second equation with the third, multiplied by −1. If the third equation is multiplied by −1, it takes the form −4x + 5y − 2z = −1 . Now let's add it to the second equation:
We got the equation x− 2y= −1 . Let's substitute the value into it x which we found earlier. Then we can determine the value y
Now we know the meanings x And y. This allows you to determine the value z. Let's use one of the equations included in the system:
Thus, the triple of values (1; 1; 1) is the solution to our system. By checking we make sure that these values satisfy the system:
Problems on composing systems of linear equations
The task of composing systems of equations is solved by entering several variables. Next, equations are compiled based on the conditions of the problem. From the compiled equations they form a system and solve it. Having solved the system, it is necessary to check whether its solution satisfies the conditions of the problem.
Problem 1. A Volga car drove out of the city to the collective farm. She returned back along another road, which was 5 km shorter than the first. In total, the car traveled 35 km round trip. How many kilometers is the length of each road?
Solution
Let x— length of the first road, y- length of the second. If the car traveled 35 km round trip, then the first equation can be written as x+ y= 35. This equation describes the sum of the lengths of both roads.
It is said that the car returned along a road that was 5 km shorter than the first one. Then the second equation can be written as x− y= 5. This equation shows that the difference between the road lengths is 5 km.
Or the second equation can be written as x= y+ 5. We will use this equation.
Because the variables x And y in both equations denote the same number, then we can form a system from them:
Let's solve this system using some of the previously studied methods. In this case, it is convenient to use the substitution method, since in the second equation the variable x already expressed.
Substitute the second equation into the first and find y
Let's substitute the found value y in the second equation x= y+ 5 and we'll find x
The length of the first road was indicated through the variable x. Now we have found its meaning. Variable x is equal to 20. This means that the length of the first road is 20 km.
And the length of the second road was indicated by y. The value of this variable is 15. This means the length of the second road is 15 km.
Let's check. First, let's make sure that the system is solved correctly:
Now let’s check whether the solution (20; 15) satisfies the conditions of the problem.
It was said that the car traveled a total of 35 km round trip. We add the lengths of both roads and make sure that the solution (20; 15) satisfies this condition: 20 km + 15 km = 35 km
The following condition: the car returned back along another road, which was 5 km shorter than the first . We see that solution (20; 15) also satisfies this condition, since 15 km is shorter than 20 km by 5 km: 20 km − 15 km = 5 km
When composing a system, it is important that the variables represent the same numbers in all equations included in this system.
So our system contains two equations. These equations in turn contain variables x And y, which represent the same numbers in both equations, namely road lengths of 20 km and 15 km.
Problem 2. Oak and pine sleepers were loaded onto the platform, 300 sleepers in total. It is known that all oak sleepers weighed 1 ton less than all pine sleepers. Determine how many oak and pine sleepers there were separately, if each oak sleeper weighed 46 kg, and each pine sleeper 28 kg.
Solution
Let x oak and y pine sleepers were loaded onto the platform. If there were 300 sleepers in total, then the first equation can be written as x+y = 300 .
All oak sleepers weighed 46 x kg, and the pine ones weighed 28 y kg. Since oak sleepers weighed 1 ton less than pine sleepers, the second equation can be written as 28y − 46x= 1000 . This equation shows that the difference in mass between oak and pine sleepers is 1000 kg.
Tons were converted to kilograms since the mass of oak and pine sleepers was measured in kilograms.
As a result, we obtain two equations that form the system
Let's solve this system. Let us express in the first equation x. Then the system will take the form:
Substitute the first equation into the second and find y
Let's substitute y into the equation x= 300 − y and find out what it is x
This means that 100 oak and 200 pine sleepers were loaded onto the platform.
Let's check whether the solution (100; 200) satisfies the conditions of the problem. First, let's make sure that the system is solved correctly:
It was said that there were 300 sleepers in total. We add up the number of oak and pine sleepers and make sure that the solution (100; 200) satisfies this condition: 100 + 200 = 300.
The following condition: all oak sleepers weighed 1 ton less than all pine sleepers . We see that the solution (100; 200) also satisfies this condition, since 46 × 100 kg of oak sleepers is lighter than 28 × 200 kg of pine sleepers: 5600 kg − 4600 kg = 1000 kg.
Problem 3. We took three pieces of copper-nickel alloy in ratios of 2: 1, 3: 1 and 5: 1 by weight. A piece weighing 12 kg was fused from them with a ratio of copper and nickel content of 4: 1. Find the mass of each original piece if the mass of the first is twice the mass of the second.
Let us analyze two types of solutions to systems of equations:
1. Solving the system using the substitution method.
2. Solving the system by term-by-term addition (subtraction) of the system equations.
In order to solve the system of equations by substitution method you need to follow a simple algorithm:
1. Express. From any equation we express one variable.
2. Substitute. We substitute the resulting value into another equation instead of the expressed variable.
3. Solve the resulting equation with one variable. We find a solution to the system.
To decide system by term-by-term addition (subtraction) method need to:
1. Select a variable for which we will make identical coefficients.
2. We add or subtract equations, resulting in an equation with one variable.
3. Solve the resulting linear equation. We find a solution to the system.
The solution to the system is the intersection points of the function graphs.
Let us consider in detail the solution of systems using examples.
Example #1:
Let's solve by substitution method
Solving a system of equations using the substitution method2x+5y=1 (1 equation)
x-10y=3 (2nd equation)
1. Express
It can be seen that in the second equation there is a variable x with a coefficient of 1, which means that it is easiest to express the variable x from the second equation.
x=3+10y
2.After we have expressed it, we substitute 3+10y into the first equation instead of the variable x.
2(3+10y)+5y=1
3. Solve the resulting equation with one variable.
2(3+10y)+5y=1 (open the brackets)
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=-0.2
The solution to the equation system is the intersection points of the graphs, therefore we need to find x and y, because the intersection point consists of x and y. Let's find x, in the first point where we expressed it, we substitute y there.
x=3+10y
x=3+10*(-0.2)=1
It is customary to write points in the first place we write the variable x, and in the second place the variable y.
Answer: (1; -0.2)
Example #2:
Let's solve using the term-by-term addition (subtraction) method.
Solving a system of equations using the addition method3x-2y=1 (1 equation)
2x-3y=-10 (2nd equation)
1. We choose a variable, let’s say we choose x. In the first equation, the variable x has a coefficient of 3, in the second - 2. We need to make the coefficients the same, for this we have the right to multiply the equations or divide by any number. We multiply the first equation by 2, and the second by 3 and get a total coefficient of 6.
3x-2y=1 |*2
6x-4y=2
2x-3y=-10 |*3
6x-9y=-30
2. Subtract the second from the first equation to get rid of the variable x. Solve the linear equation.
__6x-4y=2
5y=32 | :5
y=6.4
3. Find x. We substitute the found y into any of the equations, let’s say into the first equation.
3x-2y=1
3x-2*6.4=1
3x-12.8=1
3x=1+12.8
3x=13.8 |:3
x=4.6
The intersection point will be x=4.6; y=6.4
Answer: (4.6; 6.4)
Do you want to prepare for exams for free? Tutor online for free. No joke.
Let us first consider the case when the number of equations is equal to the number of variables, i.e. m = n. Then the matrix of the system is square, and its determinant is called the determinant of the system.
Inverse matrix method
Let us consider in general form the system of equations AX = B with a non-degenerate square matrix A. In this case, there is an inverse matrix A -1. Let's multiply both sides by A -1 on the left. We get A -1 AX = A -1 B. Hence EX = A -1 B and
The last equality is a matrix formula for finding solutions to such systems of equations. The use of this formula is called the inverse matrix method
For example, let’s use this method to solve the following system:
;
At the end of solving the system, you can check by substituting the found values into the system equations. In doing so, they must turn into true equalities.
For the example considered, let's check:
Method for solving systems of linear equations with a square matrix using Cramer's formulas
Let n= 2:
If we multiply both sides of the first equation by a 22, and both sides of the second by (-a 12), and then add the resulting equations, then we eliminate the variable x 2 from the system. Similarly, you can eliminate the variable x 1 (by multiplying both sides of the first equation by (-a 21), and both sides of the second by a 11). As a result, we get the system:
The expression in brackets is the determinant of the system
Let's denote
Then the system will take the form:
From the resulting system it follows that if the determinant of the system is 0, then the system will be consistent and definite. Its only solution can be calculated using the formulas:
If = 0, a 1 0 and/or 2 0, then the system equations will take the form 0*x 1 = 2 and/or 0*x 1 = 2. In this case, the system will be inconsistent.
In the case when = 1 = 2 = 0, the system will be consistent and indefinite (will have an infinite number of solutions), since it will take the form:
Cramer's theorem(we will omit the proof). If the determinant of the matrix of a system of equations is not equal to zero, then the system has a unique solution, determined by the formulas:
,
where j is the determinant of the matrix obtained from matrix A by replacing the j-th column with a column of free terms.
The above formulas are called Cramer formulas.
As an example, let’s use this method to solve a system that was previously solved using the inverse matrix method:
Disadvantages of the considered methods:
1) significant labor intensity (calculating determinants and finding the inverse matrix);
2) limited scope (for systems with a square matrix).
Real economic situations are often modeled by systems in which the number of equations and variables is quite significant, and there are more equations than variables. Therefore, in practice, the following method is more common.
Gaussian method (method of sequential elimination of variables)
This method is used to solve a system of m linear equations with n variables in general view. Its essence lies in applying a system of equivalent transformations to the extended matrix, with the help of which the system of equations is transformed to a form when its solutions become easy to find (if any).
This is the kind in which the left upper part The matrix of the system will be a stepped matrix. This is achieved using the same techniques that were used to obtain a step matrix to determine the rank. In this case, elementary transformations are applied to the extended matrix, which will allow one to obtain an equivalent system of equations. After this, the expanded matrix will take the form:
Obtaining such a matrix is called straight forward Gauss method.
Finding the values of variables from the corresponding system of equations is called in reverse Gauss method. Let's consider it.
Note that the last (m – r) equations will take the form:
If at least one of the numbers 
is not equal to zero, then the corresponding equality will be false, and the entire system will be inconsistent.
Therefore, for any joint system 
. In this case, the last (m – r) equations for any values of the variables will be identities 0 = 0, and they can be ignored when solving the system (simply discard the corresponding rows).
After this, the system will look like:
Let us first consider the case when r=n. Then the system will take the form:
From the last equation of the system, x r can be uniquely found.
Knowing x r, we can unambiguously express x r -1 from it. Then, from the previous equation, knowing x r and x r -1, we can express x r -2, etc. up to x 1 .
So, in this case the system will be joint and determined.
Now consider the case when r
From this equation we can express the basic variable x r in terms of non-basic ones:
The penultimate equation will look like:
By substituting the resulting expression instead of x r, it will be possible to express the basic variable x r -1 in terms of non-basic ones. Etc. to variablex 1 . To obtain a solution to the system, you can equate non-basic variables to arbitrary values and then calculate the basic variables using the resulting formulas. Thus, in this case the system will be consistent and indefinite (have an infinite number of solutions).
For example, let's solve the system of equations:
We will call the set of basic variables basis systems. We will also call the set of columns of coefficients for them basis(base columns), or basic minor system matrices. The solution of the system in which all non-basic variables are equal to zero will be called basic solution.
In the previous example, the basic solution will be (4/5; -17/5; 0; 0) (the variables x 3 and x 4 (c 1 and c 2) are set to zero, and the basic variables x 1 and x 2 are calculated through them) . To give an example of a non-basic solution, we need to equate x 3 and x 4 (c 1 and c 2) to arbitrary numbers that are not simultaneously zero, and calculate the remaining variables through them. For example, with 1 = 1 and 2 = 0, we obtain a non-basic solution - (4/5; -12/5; 1; 0). By substitution it is easy to verify that both solutions are correct.
It is obvious that in an indefinite system there can be an infinite number of non-basic solutions. How many basic solutions can there be? Each row of the transformed matrix must correspond to one basis variable. There are n variables in the problem, and r base lines. Therefore, the number of all possible sets of basic variables cannot exceed the number of combinations of n by 2. It may be less than 
, because it is not always possible to transform the system to such a form that this particular set of variables is the basis.
What kind is this? This is the type when the matrix formed from columns of coefficients for these variables will be stepped, and at the same time will consist of r rows. Those. the rank of the coefficient matrix for these variables must be equal to r. It cannot be greater, since the number of columns is equal. If it turns out to be less than r, then this indicates a linear dependence of the columns on the variables. Such columns cannot form a basis.
Let's consider what other basic solutions can be found in the example discussed above. To do this, consider all possible combinations of four variables, two basic ones each. There will be such combinations 
, and one of them (x 1 and x 2) has already been considered.
Let's take the variables x 1 and x 3. Let us find the rank of the matrix of coefficients for them:
Since it is equal to two, they can be basic. Let us equate the non-basic variables x 2 and x 4 to zero: x 2 = x 4 = 0. Then from the formula x 1 = 4/5 – (1/5)*x 4 it follows that x 1 = 4/5, and from the formula x 2 = -17/5 + x 3 - - (7/5)*x 4 = -17/5 + x 3 it follows that x 3 = x 2 +17/5 = 17/5. Thus, we get the basic solution (4/5; 0; 17/5; 0).
Similarly, you can obtain basic solutions for the basic variables x 1 and x 4 – (9/7; 0; 0; -17/7); x 2 and x 4 – (0; -9; 0; 4); x 3 and x 4 – (0; 0; 9; 4).
The variables x 2 and x 3 in this example cannot be taken as basic ones, since the rank of the corresponding matrix is equal to one, i.e. less than two:
.
Another approach to determining whether or not it is possible to construct a basis from certain variables is also possible. When solving the example, as a result of transforming the system matrix to a stepwise form, it took the form:
By selecting pairs of variables, it was possible to calculate the corresponding minors of this matrix. It is easy to verify that for all pairs except x 2 and x 3 they are not equal to zero, i.e. the columns are linearly independent. And only for columns with variables x 2 and x 3 
, which indicates their linear dependence.
Let's look at another example. Let's solve the system of equations
So, the equation corresponding to the third row of the last matrix is contradictory - it resulted in the incorrect equality 0 = -1, therefore, this system is inconsistent.
Jordan-Gauss method 3 is a development of the Gaussian method. Its essence is that the extended matrix of the system is transformed to a form where the coefficients of the variables form an identity matrix up to permutation of rows or columns 4 (where r is the rank of the system matrix).
Let's solve the system using this method:
Let's consider the extended matrix of the system:
In this matrix we select a unit element. For example, the coefficient for x 2 in the third constraint is 5. Let's ensure that the remaining rows in this column contain zeros, i.e. let's make the column single. During the transformation process we will call this columnpermissive(leading, key). The third limitation (third line) we will also call permissive. Myself element, which stands at the intersection of the resolving row and column (here it is one), is also called permissive.
The first line now contains the coefficient (-1). To get a zero in its place, multiply the third line by (-1) and subtract the result from the first line (i.e. simply add the first line to the third).
The second line contains the coefficient 2. To get zero in its place, multiply the third line by 2 and subtract the result from the first line.
The result of the transformation will look like:
From this matrix it is clearly visible that one of the first two restrictions can be crossed out (the corresponding rows are proportional, i.e. these equations follow from each other). Let's cross out, for example, the second:
So, the new system has two equations. A single column (second) is obtained, and the unit here appears in the second row. Let us remember that the second equation of the new system will correspond to the basic variable x 2.
Let's choose a base variable for the first row. This can be any variable except x 3 (because for x 3 the first constraint has a zero coefficient, i.e. the set of variables x 2 and x 3 cannot be basic here). You can take the first or fourth variable.
Let's choose x 1. Then the resolving element will be 5, and both sides of the resolving equation will have to be divided by five to get one in the first column of the first row.
Let's ensure that the remaining rows (i.e., the second row) have zeros in the first column. Since now the second line contains not zero, but 3, we need to subtract from the second line the elements of the transformed first line, multiplied by 3:
From the resulting matrix, one can directly extract one basic solution by equating non-basic variables to zero, and basic ones to the free terms in the corresponding equations: (0.8; -3.4; 0; 0). You can also derive general formulas expressing basic variables through non-basic ones: x 1 = 0.8 – 1.2 x 4; x 2 = -3.4 + x 3 + 1.6x 4. These formulas describe the entire infinite set of solutions to the system (equating x 3 and x 4 to arbitrary numbers, you can calculate x 1 and x 2).
Note that the essence of the transformations at each stage of the Jordan-Gauss method was as follows:
1) the resolution line was divided by the resolution element to obtain a unit in its place,
2) from all other rows, the transformed resolution was subtracted, multiplied by the element that was in the given row in the resolution column, to get a zero in place of this element.
Let us consider again the transformed extended matrix of the system:
From this record it is clear that the rank of the matrix of system A is equal to r.
In the course of our reasoning, we established that the system will be cooperative if and only if 
. This means that the extended matrix of the system will look like:
By discarding zero rows, we obtain that the rank of the extended matrix of the system is also equal to r.
Kronecker-Capelli theorem. A system of linear equations is consistent if and only if the rank of the system's matrix is equal to the rank of the extended matrix of this system.
Recall that the rank of a matrix is equal to the maximum number of its linearly independent rows. It follows from this that if the rank of the extended matrix is less than the number of equations, then the equations of the system are linearly dependent, and one or more of them can be excluded from the system (since they are a linear combination of the others). A system of equations will be linearly independent only if the rank of the extended matrix is equal to the number of equations.
Moreover, for simultaneous systems of linear equations, it can be argued that if the rank of the matrix is equal to the number of variables, then the system has a unique solution, and if it is less than the number of variables, then the system is indefinite and has infinitely many solutions.
1For example, let there be five rows in the matrix (the original row order is 12345). We need to change the second line and the fifth. In order for the second line to take the place of the fifth and “move” down, we successively change the adjacent lines three times: the second and third (13245), the second and fourth (13425) and the second and fifth (13452). Then, in order for the fifth row to take the place of the second in the original matrix, it is necessary to “shift” the fifth row upward by only two consecutive changes: the fifth and fourth rows (13542) and the fifth and third (15342).
2Number of combinations from n to r 
they call the number of all different r-element subsets of an n-element set (those that have different compositions of elements are considered different sets; the order of selection is not important). It is calculated using the formula: 
. Let us recall the meaning of the sign “!” (factorial): 
0!=1.)
3 Since this method is more common than the previously discussed Gaussian method, and is essentially a combination of the forward and backward steps of the Gaussian method, it is also sometimes called the Gaussian method, omitting the first part of the name.
4For example, 
.
5If there were no units in the system matrix, then it would be possible, for example, to divide both sides of the first equation by two, and then the first coefficient would become unity; or the like
Using this mathematical program, you can solve a system of two linear equations with two variables using the substitution method and the addition method.
The program not only gives the answer to the problem, but also provides a detailed solution with explanations of the solution steps in two ways: the substitution method and the addition method.
This program can be useful for high school students in general education schools when preparing for tests and exams, when testing knowledge before the Unified State Exam, and for parents to control the solution of many problems in mathematics and algebra. Or maybe it’s too expensive for you to hire a tutor or buy new textbooks? Or do you just want to get your math or algebra homework done as quickly as possible? In this case, you can also use our programs with detailed solutions.
In this way, you can conduct your own training and/or training of your younger brothers or sisters, while the level of education in the field of solving problems increases.
Rules for entering equations
Any Latin letter can act as a variable.
For example: \(x, y, z, a, b, c, o, p, q\), etc.
When entering equations you can use parentheses. In this case, the equations are first simplified. The equations after simplifications must be linear, i.e. of the form ax+by+c=0 with the accuracy of the order of elements.
For example: 6x+1 = 5(x+y)+2
In equations, you can use not only whole numbers, but also fractions in the form of decimals and ordinary fractions.
Rules for entering decimal fractions.
The integer and fractional parts in decimal fractions can be separated by either a period or a comma.
For example: 2.1n + 3.5m = 55
Rules for entering ordinary fractions.
Only a whole number can act as the numerator, denominator and integer part of a fraction.
The denominator cannot be negative.
When entering a numerical fraction, the numerator is separated from the denominator by a division sign: /
The whole part is separated from the fraction by the ampersand sign: &
Examples.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3.5p - 2&1/8q)
Solve system of equations
It was discovered that some scripts necessary to solve this problem were not loaded, and the program may not work.
You may have AdBlock enabled.
In this case, disable it and refresh the page.
For the solution to appear, you need to enable JavaScript.
Here are instructions on how to enable JavaScript in your browser.
Because There are a lot of people willing to solve the problem, your request has been queued.
In a few seconds the solution will appear below.
Please wait sec...
If you noticed an error in the solution, then you can write about this in the Feedback Form.
Don't forget indicate which task you decide what enter in the fields.
Our games, puzzles, emulators:
A little theory.
Solving systems of linear equations. Substitution method
The sequence of actions when solving a system of linear equations using the substitution method:
1) express one variable from some equation of the system in terms of another;
2) substitute the resulting expression into another equation of the system instead of this variable;
$$ \left\( \begin(array)(l) 3x+y=7 \\ -5x+2y=3 \end(array) \right. $$
Let's express y in terms of x from the first equation: y = 7-3x. Substituting the expression 7-3x into the second equation instead of y, we obtain the system:
$$ \left\( \begin(array)(l) y = 7-3x \\ -5x+2(7-3x)=3 \end(array) \right. $$
It is easy to show that the first and second systems have the same solutions. In the second system, the second equation contains only one variable. Let's solve this equation:
$$ -5x+2(7-3x)=3 \Rightarrow -5x+14-6x=3 \Rightarrow -11x=-11 \Rightarrow x=1 $$
Substituting 1 instead of x into the equality y=7-3x, we find the corresponding value of y:
$$ y=7-3 \cdot 1 \Rightarrow y=4 $$
Pair (1;4) - solution of the system
Systems of equations in two variables that have the same solutions are called equivalent. Systems that do not have solutions are also considered equivalent.
Solving systems of linear equations by addition
Let's consider another way to solve systems of linear equations - the addition method. When solving systems in this way, as well as when solving by substitution, we move from this system to another, equivalent system, in which one of the equations contains only one variable.
The sequence of actions when solving a system of linear equations using the addition method:
1) multiply the equations of the system term by term, selecting factors so that the coefficients of one of the variables become opposite numbers;
2) add the left and right sides of the system equations term by term;
3) solve the resulting equation with one variable;
4) find the corresponding value of the second variable.
Example. Let's solve the system of equations:
$$ \left\( \begin(array)(l) 2x+3y=-5 \\ x-3y=38 \end(array) \right. $$
In the equations of this system, the coefficients of y are opposite numbers. By adding the left and right sides of the equations term by term, we obtain an equation with one variable 3x=33. Let's replace one of the equations of the system, for example the first one, with the equation 3x=33. Let's get the system
$$ \left\( \begin(array)(l) 3x=33 \\ x-3y=38 \end(array) \right. $$
From the equation 3x=33 we find that x=11. Substituting this x value into the equation \(x-3y=38\) we get an equation with the variable y: \(11-3y=38\). Let's solve this equation:
\(-3y=27 \Rightarrow y=-9 \)
Thus, we found the solution to the system of equations by addition: \(x=11; y=-9\) or \((11;-9)\)
Taking advantage of the fact that in the equations of the system the coefficients of y are opposite numbers, we reduced its solution to the solution of an equivalent system (by summing both sides of each of the equations of the original system), in which one of the equations contains only one variable.
Books (textbooks) Abstracts of the Unified State Examination and the Unified State Examination tests online Games, puzzles Plotting graphs of functions Spelling dictionary of the Russian language Dictionary of youth slang Catalog of Russian schools Catalog of secondary educational institutions of Russia Catalog of Russian universities List of tasks
