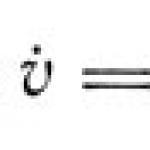Mis on ringi keskne ja sisse kirjutatud nurk. Ring. Kesknurk

Sissekirjutatud nurk, probleemi teooria. Sõbrad! Selles artiklis räägime ülesannetest, mille lahendamiseks on vaja teada sisse kirjutatud nurga omadusi. See on terve ülesannete rühm, need sisalduvad eksamil. Enamik neist lahendatakse väga lihtsalt, ühe sammuga.

On raskemaid ülesandeid, kuid need ei valmista teile palju raskusi, peate teadma sisse kirjutatud nurga omadusi. Järk-järgult analüüsime kõiki ülesannete prototüüpe, kutsun teid blogisse!

Nüüd vajalik teooria. Tuletage meelde, milline on keskne ja sisse kirjutatud nurk, kõõl, kaar, millele need nurgad tuginevad:

Ringi kesknurka nimetatakse tasaseks nurgakstipp selle keskel.
Ringi osa, mis asub tasase nurga seesnimetatakse ringikaareks.
Ringjoone kaare kraadimõõt on kraadimõõtvastav kesknurk.
Nurka nimetatakse ringi sisse kirjutatud, kui nurga tipp asubringil ja nurga küljed lõikuvad selle ringiga.

Nimetatakse sirglõiku, mis ühendab kahte ringi punktiakord. Pikim akord läbib ringi keskpunkti ja seda kutsutakseläbimõõt.

Ringi sisse kirjutatud nurkade ülesannete lahendamisekspeate teadma järgmisi omadusi:

1. Sissekirjutatud nurk on võrdne poole sama kaare kesknurgaga.

2. Kõik samal kaarel põhinevad sisse kirjutatud nurgad on võrdsed.

3. Kõik samal kõõlul põhinevad sissekirjutatud nurgad, mille tipud asuvad selle kõõlu ühel küljel, on võrdsed.

4. Kõik samal kõõlul põhinevad nurgapaarid, mille tipud asuvad kõõlu vastaskülgedel, annavad kokku 180 °.

Järeldus: ringi sisse kirjutatud nelinurga vastasnurgad annavad kokku 180 kraadi.

5. Kõik läbimõõdul põhinevad sisse kirjutatud nurgad on sirged.

Üldiselt on see omadus omaduse (1) tagajärg, see on selle konkreetne juhtum. Vaata - kesknurk on võrdne 180 kraadiga (ja see kujunenud nurk pole midagi muud kui läbimõõt), mis tähendab, et esimese omaduse järgi on sisse kirjutatud nurk C võrdne selle poolega, see tähendab 90 kraadi.

Selle omaduse tundmine aitab lahendada paljusid probleeme ja võimaldab sageli vältida tarbetuid arvutusi. Olles seda hästi omandanud, suudate suuliselt lahendada enam kui pooled seda tüüpi probleemidest. Kaks tagajärge, mida saab teha:

Järeldus 1: kui kolmnurk on kirjutatud ringi ja selle üks külg langeb kokku selle ringi läbimõõduga, siis on kolmnurk täisnurkne (täisnurga tipp asub ringil).

Järeldus 2: täisnurkse kolmnurga ümber piiritletud ringi keskpunkt langeb kokku selle hüpotenuusi keskpunktiga.

Paljud stereomeetriliste probleemide prototüübid lahendatakse ka selle omaduse ja nende tagajärgede abil. Pidage meeles tõsiasja ennast: kui ringi läbimõõt on sisse kirjutatud kolmnurga külg, siis see kolmnurk on täisnurkne (läbimõõdu vastasnurk on 90 kraadi). Kõik muud järeldused ja tagajärjed saate ise teha, neid pole vaja õpetada.

Reeglina on pooled sisse kirjutatud nurga ülesanded antud visandiga, kuid ilma märgeteta. Arutlusprotsessi mõistmiseks ülesannete lahendamisel (artiklis allpool) tutvustatakse tippude (nurkade) tähistusi. Eksamil ei saa te seda teha.Kaaluge ülesandeid:

Mis on terav nurk, mis lõikab ringi raadiusega võrdse kõõlu? Esitage oma vastus kraadides.

Ehitame etteantud sissekirjutatud nurga jaoks kesknurga, tähistame tippe:

Vastavalt ringi sisse kirjutatud nurga omadusele:

Nurk AOB on võrdne 60 0, kuna kolmnurk AOB on võrdkülgne ja võrdkülgse kolmnurga kõik nurgad on võrdsed 60 0 . Kolmnurga küljed on võrdsed, kuna tingimus ütleb, et kõõl on võrdne raadiusega.

Seega on sisse kirjutatud nurk DIA 30 0 .

Vastus: 30

Leidke kõõl, millele toetub nurk 30 0, mis on kantud raadiusega 3 ringi.

See on sisuliselt (eelmise) pöördprobleem. Ehitame kesknurga.

See on kaks korda suurem kui kirjutatud, see tähendab, et nurk AOB on 60 0 . Sellest võime järeldada, et kolmnurk AOB on võrdkülgne. Seega on akord võrdne raadiusega, see tähendab kolmega.

Vastus: 3

Ringjoone raadius on 1. Leidke nüri sissekirjutatud nurga väärtus kahe juurega võrdse kõõlu põhjal. Esitage oma vastus kraadides.

Ehitame kesknurga:

Teades raadiust ja kõõlu, leiame kesknurga DIA. Seda saab teha koosinusseadust kasutades. Teades kesknurka, leiame hõlpsasti sisse kirjutatud nurga ACB.

Koosinusteoreem: kolmnurga mis tahes külje ruut on võrdne kahe teise külje ruutude summaga, ilma nende külgede korrutist kahekordistamata nendevahelise nurga koosinusega.

Seetõttu on teine kesknurk 360 0 – 90 0 = 270 0 .

Vastavalt sisse kirjutatud nurga omadusele on nurk DIA võrdne selle poolega, see tähendab 135 kraadi.

Vastus: 135

Leidke kõõl, millele on raadiusega ringi sisse kirjutatud nurk 120 kraadi, kolme juur.

Ühendage punktid A ja B ringi keskpunktiga. Nimetagem seda O:

Me teame raadiust ja sisse kirjutatud nurka DIA. Leiame kesknurga AOB (suurem kui 180 kraadi), seejärel leiame nurga AOB kolmnurgast AOB. Ja siis koosinusteoreemi kasutades arvuta AB.

Sissekirjutatud nurga omaduse järgi on kesknurk AOB (mis on suurem kui 180 kraadi) võrdne kahekordse sisse kirjutatud nurgaga, see tähendab 240 kraadi. See tähendab, et nurk AOB kolmnurgas AOB on 360 0 - 240 0 = 120 0 .

Koosinuse seaduse järgi:

Vastus: 3

Leidke sisse kirjutatud nurk kaare põhjal, mis on 20% ringist. Esitage oma vastus kraadides.

Sissekirjutatud nurga omaduse järgi on see poole väiksem kui samal kaarel põhinevast kesknurgast, antud juhul räägime kaarest AB.

Öeldakse, et kaar AB on 20 protsenti ümbermõõdust. See tähendab, et kesknurk AOB on samuti 20 protsenti 360 0-st.* Ring on 360 kraadine nurk. Tähendab,

Seega on sisse kirjutatud nurk ACB 36 kraadi.

Vastus: 36

ringi kaar AC, mis ei sisalda punkte B, on 200 kraadi. Ja ringi BC kaar, mis ei sisalda punkte A, on 80 kraadi. Leidke sisse kirjutatud nurk ACB. Esitage oma vastus kraadides.

Tähistagem selguse huvides kaared, mille nurkmõõdud on antud. 200 kraadile vastav kaar on sinine, 80 kraadile vastav kaar on punane, ülejäänud ring on kollane.

Seega on kaare AB aste (kollane) ja seega ka kesknurk AOB: 360 0 – 200 0 – 80 0 = 80 0 .

Sissekirjutatud nurk DAB on pool kesknurgast AOB, st võrdne 40 kraadiga.

Vastus: 40

Mis on sisse kirjutatud nurk, mis põhineb ringi läbimõõdul? Esitage oma vastus kraadides.

kesknurk on kahe raadiusega moodustatud nurk ringid. Kesknurga näide on nurk AOB, BOC, COE jne.

KOHTA kesknurk Ja kaar poolte vahel sõlmitud, ütlevad nad, et nemad vastamaüksteist.

1. kui kesksed nurgad kaared on võrdsed.

2. kui kesksed nurgad ei ole võrdsed, siis vastab suurem neist suuremale kaar.

Olgu AOB ja COD kaks kesksed nurgad, võrdne või ebavõrdne. Pöörake sektor AOB ümber keskpunkti noolega näidatud suunas nii, et raadius OA langeks kokku OC-ga, siis, kui kesknurgad on võrdsed, siis raadius OA ühtib OD-ga ja kaar AB kaarega CD.

Nii et need kaared on võrdsed.

Kui kesksed nurgad ei ole võrdsed, siis ei lähe raadius OB mööda OD, vaid mööda mõnda muud suunda, näiteks piki OE või OF. Mõlemal juhul vastab suurem nurk ilmselt suuremale kaarele.

Teoreem, mille ühe ringi jaoks tõestasime, jääb tõeseks võrdsed ringid, sest sellised ringid ei erine üksteisest, välja arvatud oma positsiooni poolest.

Vastupidised pakkumised saab ka tõeks . Samas ringis või võrdsetes ringides:

1. kui kaared on võrdsed, siis vastavad kesksed nurgad on võrdsed.

2. kui kaared ei ole võrdsed, siis vastab suurem neist suuremale kesknurk.

Samas ringis või võrdsetes ringides on kesknurgad seotud nende vastavate kaarega. Või parafraseerides saame selle kesknurgaks proportsionaalne sellele vastav kaar.

Nurk ABC on sisse kirjutatud nurk. See toetub kaarele AC, mis on selle külgede vahele suletud (joonis 330).

Teoreem. Sissekirjutatud nurka mõõdetakse poole kaarega, mille see lõikab.

Seda tuleks mõista järgmiselt: sisse kirjutatud nurk sisaldab sama palju nurgakraade, minuteid ja sekundeid kui kaare kraadid, minutid ja sekundid sisalduvad kaare pooles, millel see toetub.

Selle teoreemi tõestamisel peame arvestama kolme juhtumiga.

Esimene juhtum. Ringi keskpunkt asub sisse kirjutatud nurga küljel (joonis 331).

Olgu ∠ABC sisse kirjutatud nurk ja ringi O keskpunkt asub küljel BC. On vaja tõestada, et seda mõõdetakse poole vahelduvkaare võrra.

Ühendage punkt A ringi keskpunktiga. Sama ringi raadiusteks saame võrdhaarsed $\Delta$AOB, milles AO = OB. Seetõttu ∠A = ∠B.

∠AOC on kolmnurgast AOB väline, seega ∠AOC = ∠A + ∠B ja kuna nurgad A ja B on võrdsed, on ∠B 1/2 ∠AOC.

Kuid ∠AOC mõõdetakse kaare vahelduvvooluga, seega ∠B mõõdetakse poole vahelduvkaarega.

Näiteks kui $\breve(AC)$ sisaldab 60°18', siis ∠B sisaldab 30°9'.

Teine juhtum. Ringi keskpunkt asub sisse kirjutatud nurga külgede vahel (joonis 332).

Olgu ∠ABD sisse kirjutatud nurk. Ringi O keskpunkt asub selle külgede vahel. On vaja tõestada, et ∠ABD mõõdetakse poole kaare võrra AD.

Selle tõestamiseks joonestame läbimõõdu BC. Nurk ABD jagatud kaheks nurgaks: ∠1 ja ∠2.

∠1 mõõdetakse poole võrra kaarest AC ja ∠2 mõõdetakse poole kaarega CD, seega mõõdetakse kogu ∠ABD 1/2 $\breve(AC)$ + 1/2 $ \breve(CD)$, st pool kaarest AD.

Näiteks kui $\breve(AD)$ sisaldab 124°, siis ∠B sisaldab 62°.

Kolmas juhtum. Ringi keskpunkt asub väljaspool sisse kirjutatud nurka (joonis 333).

Olgu ∠MAD sisse kirjutatud nurk. Ringi O keskpunkt asub väljaspool nurka. On vaja tõestada, et ∠MAD mõõdetakse poole kaare MD võrra.

Selle tõestamiseks joonistame läbimõõdu AB. ∠MAD = ∠MAB – ∠DAB. Kuid ∠MAB mõõdab 1/2 $\breve(MB)$ ja ∠DAB mõõdab 1/2 $\breve(DB)$.

Seetõttu mõõdab ∠MAD 1/2 ($\breve(MB) - \breve(DB))$, st 1/2 $\breve(MD)$.

Näiteks kui $\breve(MD)$ sisaldab 48° 38", siis ∠MAD sisaldab 24° 19' 8".

Tagajärjed
1. Kõik samal kaarel põhinevad sisse kirjutatud nurgad on üksteisega võrdsed, kuna neid mõõdetakse poolega samast kaarest (joonis 334, a).

2. Läbimõõdul põhinev sisse kirjutatud nurk on täisnurk, kuna see põhineb poolel ringil. Pool ringist sisaldab 180 kaarekraadi, mis tähendab, et läbimõõdul põhinev nurk sisaldab 90 nurgakraadi (joonis 334, b).

RING JA RING. SILINDER.

§ 76. Sissekirjutatud ja MÕNED MUUD NURgad.

1. Sissekirjutatud nurk.

Nurka, mille tipp asub ringil ja mille küljed on kõõlud, nimetatakse sissekirjutatud nurgaks.

Nurk ABC on sisse kirjutatud nurk. See toetub selle külgede vahele suletud kaarele AC (joonis 330).

Teoreem. Sissekirjutatud nurka mõõdetakse poole kaarega, mille see lõikab.

Seda tuleks mõista järgmiselt: sisse kirjutatud nurk sisaldab sama palju nurgakraade, minuteid ja sekundeid kui kaare kraadid, minutid ja sekundid sisalduvad kaare pooles, millel see toetub.

Selle teoreemi tõestamisel peame arvestama kolme juhtumiga.

Esimene juhtum. Ringi keskpunkt asub sisse kirjutatud nurga küljel (joonis 331).

Las olla / ABC on sisse kirjutatud nurk ja ringi O keskpunkt asub küljel BC. On vaja tõestada, et seda mõõdetakse poole vahelduvkaare võrra.

Ühendage punkt A ringi keskpunktiga. Hangi võrdhaarsed /\ AOB, milles
AO = OB, sama ringi raadiustena. Järelikult / A = / IN. / AOC on kolmnurgast AOB väline, seega / AOC = / A+ / B (§ 39 punkt 2), ja kuna nurgad A ja B on võrdsed, siis / B on 1/2 / AOC.

Aga / AOC mõõdetakse vahelduvvoolu kaare abil, seetõttu / B mõõdetakse poole vahelduvvoolukaarest.

Näiteks kui AC sisaldab 60° 18", siis / B sisaldab 30°9".

Teine juhtum. Ringi keskpunkt asub sisse kirjutatud nurga külgede vahel (joonis 332).

Las olla / ABD on sisse kirjutatud nurk. Ringi O keskpunkt asub selle külgede vahel. Seda on vaja tõestada / ABD-d mõõdetakse poole võrra AD kaarest.

Selle tõestamiseks joonistagem BC läbimõõt. Nurk ABD jagatud kaheks nurgaks: / 1 ja / 2.

/ 1 mõõdetakse poole vahelduvvoolu kaarest ja / 2 mõõdetakse poole CD-kaarega, seega kogu / ABD mõõdetakse 1/2 AC + 1/2 CD, st pool AD kaarest.
Näiteks kui AD sisaldab 124°, siis / B sisaldab 62°.

Kolmas juhtum. Ringi keskpunkt asub väljaspool sisse kirjutatud nurka (joonis 333).

Las olla / MAd – sisse kirjutatud nurk. Ringi O keskpunkt asub väljaspool nurka. Seda on vaja tõestada / MAD-i mõõdetakse poole võrra MD kaarest.

Selle tõestamiseks joonistame läbimõõdu AB. / MAd = / MAV- / DAB. Aga / MAV-i mõõdetakse 1/2 MV ja / DAB mõõdetakse 1/2 DB. Järelikult / MAD mõõdetakse
1/2 (MB - DB), st 1/2 MD.
Näiteks kui MD sisaldab 48° 38"16", siis / MAD sisaldab 24° 19" 8".

Tagajärjed. üks. Kõik samal kaarel põhinevad sisse kirjutatud nurgad on üksteisega võrdsed, kuna neid mõõdetakse poolega samast kaarest (Joonis 334, a).

2. Puutuja ja akordi moodustatud nurk.

Teoreem. Puutuja ja kõõlu moodustatud nurka mõõdetakse poole selle külgede vahele jäävast kaarest.

Las olla / CAB koosneb akordist SA ja puutujast AB (joonis 335). On vaja tõestada, et seda mõõdetakse poole SA-ga. Joonistame joone CD läbi punkti C || AB. Sisse kirjutatud / ACD-d mõõdetakse poole võrra kaarest AD, kuid AD = CA, kuna need jäävad puutuja ja sellega paralleelse kõõlu vahele. Järelikult / DCA-d mõõdetakse poole CA kaarest. Alates sellest / CAB = / DCA, siis mõõdetakse ka pool CA kaarest.

Harjutused.

1. Leia jooniselt 336 ringi puutujad.

2. Tõesta vastavalt joonisele 337 a, et nurk ADC mõõdetakse poole võrra kaare AC ja BK summast.

3. Tõesta joonise 337, b järgi, et nurka AMB mõõdetakse kaare AB ja CE poolvahega.

4. Läbi punkti A, mis asub ringi sees, tõmmake joonestuskolmnurga abil kõõl nii, et see jaguneb punktis A pooleks.

5. Kasutades joonistuskolmnurka, jaga kaar 2, 4, 8... võrdseks osaks.

6. Kirjeldage etteantud raadiusega kahte etteantud punkti läbivat ringjoont. Kui palju on probleemil lahendusi?

7. Mitu ringi saab läbi antud punkti tõmmata?

Sissekirjutatud ja kesknurga mõiste

Tutvustame esmalt kesknurga mõistet.

Märkus 1

Pange tähele, et kesknurga aste on võrdne selle kaare astmega, mille see lõikab.

Nüüd tutvustame sisse kirjutatud nurga mõistet.

Definitsioon 2

Nurka, mille tipp asub ringjoonel ja mille küljed lõikuvad sama ringjoonega, nimetatakse sissekirjutatud nurgaks (joonis 2).

Joonis 2. Sissekirjutatud nurk

Sissekirjutatud nurga teoreem

1. teoreem

Sissekirjutatud nurga mõõt on pool selle kaare suurusest, mille see lõikab.

Tõestus.

Olgu meile antud ring, mille keskpunkt on punkt $O$. Tähistage sisse kirjutatud nurka $ACB$ (joonis 2). Võimalikud on järgmised kolm juhtumit:

Kiir $CO$ langeb kokku nurga mõne küljega. Olgu selleks $CB$ pool (joonis 3).

Joonis 3

Sel juhul on kaar $AB$ väiksem kui $(180)^(()^\circ )$, seega on kesknurk $AOB$ võrdne kaarega $AB$. Kuna $AO=OC=r$, on kolmnurk $AOC$ võrdhaarne. Seega on baasnurgad $CAO$ ja $ACO$ võrdsed. Kolmnurga välisnurga teoreemi kohaselt on meil: